Главная
Справочник
Видеоуроки
Тесты
Статьи
Архив
Карта сайта
Контакты
Смотрите также другие типы Задач №11 ЕГЭ по математике: 1 (на среднюю скорость), 3 (движение по воде), 4 (на работу), 5 (на движение по прямой), 6 (на прогрессии), 7 (на смеси и сплавы).
Также смотрите видеолекцию «Текстовые задачи».
Задача 1.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 19 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости другого?
Решение: + показать
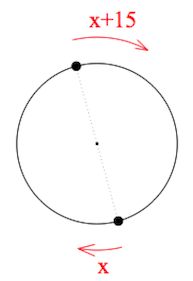
ч – время в пути мотоциклистов до первой встречи (стартовали одновременно).
км/ч – скорость одного из мотоциклистов, тогда скорость второго – 
км/ч согласно условию.
(км) – путь, пройденный мотоциклистом с меньшей скоростью до встречи. А второй мотоциклист до встречи должен будет преодолеть 
км, что на 9,5 км, согласно условию, больше пути, пройденного первым.
ч=
мин=
мин.
Задача 2.
Из одной точки круговой трассы, длина которой равна 25 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 25 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: + показать
часа первый автомобиль, ехавший со скоростью 112 км/ч, проехал 
км.
км.
км за 
(км/ч).
Задача 3.
Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Решение: + показать
км.
, то есть 
км.
км.
км. При этом его путь на 30 км больше, чем путь, проделанный велосипедистом.
(км/мин).
км/мин 
км/ч.
Задача 4.
Часы со стрелками показывают 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
Решение: + показать
За одно и тоже время минутная и часовая стрелки проходят разные расстояния.
делений.
делений.
делений
делений
часа 
мин
минут.
. Смотрите фрагмент видеолекции «Текстовые задачи»
Вы можете пройти тест по Задачам №11, задачи на движение по окружности.
Можно и так в задаче 4.
Если на часах точное время, а нужно узнать через сколько минут минутная стрелка догонит часовую в n-ый раз, то время = n*60, т.к. оборот минутная стрелка начинает сразу, потому что стоит на 12, и один раз за час догоняет часовую, т.е. совершит n оборотов, а каждый оборот – это 60 минут, т.е n*60.
Если же на часах любое число часов, а время m минут, то время = n*60+60-m, т.к. до начала оборотов минутной стрелке надо пройти (6о-m) минут, а потом совершить n оборотов.
60-45+5*60=315.
Пожалуйста! Способ решения, конечно, не один ;)
спасибо большое вам за развернутый ответ!
Теперь я поняла как можно еще решать. Самое понятное объяснение!)))
Я рада! :D
Спасибо большое!
Великолепный сайт! Буду рекомендовать ученикам. Спасибо.
Джульетта, спасибо!
Уважаемая Елена Юрьевна!!!Прошу Вашей помощи в решении такой задачки:Часы со стрелками показывают 10 часов 20 минут.Через сколько минут минутная стрелка во второй раз поравняется с часовой?-решаю я эту задачу способом как Вы задачу №4….и получаю ответ:150минут…….
Но если рассуждать логически,то стрелки поравняются во второй раз в 12.00!!значит,ответ должен быть: 100минут……
ПОМОГИТЕ,пожалуйста,разобраться,где же правильный ответ!!!!
Елена, правильный ответ – 100 минут. Я не могу вам помочь, не видя ваших рассуждений…
Видимо, закралась ошибка в ваши рассуждения. Пишите что да как…
Елена Юрьевна,вот моё решение(извините,не умею набирать формулы…):
Уважаемая Елена Юрьевна,пока набирала своё решение,увидела досадную описку…вместо знаменателя 3 у меня в решении было почему-то 2
Невнимательность моя,снова меня подвела(((
1)s(мин)=12дел/час -скорость минутной стрелки;
s(час)=1дел/час – скорость часовой стрелки.
2)за 20 мин=1/3час стрелки прошли:
s(мин)= 4 дел; s(час)= 1/3дел.
3)расстояние между стрелками в момент времени t=10ч20мин равно:
s*=6+1/3=19/3 дел.
4)Пусть s**(час)=х – расстояние,которое пройдёт часовая стрелка до момента,когда минутная стрелка догонит её во второй раз;
тогда s**(мин)=1круг+х+s*=12+x+19/3=x+55/3.
5)t(мин)=t(час)-время минутной и часовой стрелок до момента.когда минутная стрелка во второй раз поравняется с часовой
получаем уравнение:
х/1=(x+55/3)/12
12x=x+55/3
11x=55/3
x=5/3
6)t(час)=x/1=5/3час=100 мин.
Извините за беспокойство…….
С уважением,Елена.
Ну вот и славно))
Из пункта A круговой трассы выехал велосипедист, а через 8 минут следом за ним отправился мотоциклист. Через 4 минуты после отправления он догнал велосипедиста в первый раз, а еще через 24 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 12 км. Ответ дайте в км/ч. Помогите решить!
Не пробовали смотреть задачу 3 статьи?