Главная / 16 (С4) Планиметр. задачи

05 Фев 2015

Категория: 16 (С4) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 Т/Р №103 А. Ларина

Елена Репина 2015-02-05 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

В равнобедренной трапеции $ABCD$ точки $M$ и $N$ – середины оснований $BC$ и $AD$ соответственно. Отрезки $AM$ и $BN$ пересекаются в точке $P$ , а отрезки $DM$ и $CN$ пересекаются в точке $K$ .

а) Докажите, что площадь четырехугольника $PMKN$ равна сумме площадей треугольников $ABP$ и $DCK$ .

б) Найдите площадь четырехугольника $PMKN$ , если известно, что $BC=8$ , $AD=18$ , $AB=CD=13$ .

Решение:

a)

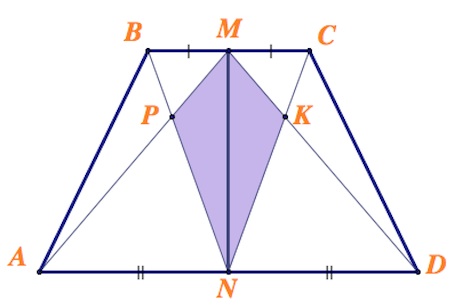
$MN$ – ось симметрии трапеции $ABCD.$

Поскольку $S_{ABP}=S_{DCK}$ , будем доказывать, например, что

$S_{PMKN}=2S_{ABP}.$

Имеем

$S_{PMKN}=2S_{AMN}-2S_{APN}.$

При этом заметим, что $S_{AMN}=S_{ABN}$ и $S_{ABN}=S_{ABP}+S_{APN}.$

Итак, $S_{PMKN}=2S_{AMN}-2S_{APN}=2(S_{ABP}+S_{APN})-2S_{APN}=2S_{ABP}.$

Что и требовалось доказать.

б) Пусть $BH_1\perp AD$ , $CH_2\perp AD$ , $PQ\perp BC$ , $PT\perp AD$ .

Очевидно, $AH_1=DH_2=5.$

Из прямоугольного треугольника $ABH_1$ находим высоту трапеции:

$BH_1=\sqrt{13^2-5^2}=12.$

Заметим, $\Delta PBM\infty \Delta PNA$ и коэффициент подобия – $4:9.$

Тогда $PT=\frac{9}{13}BH_1=\frac{108}{13}$ .

Из пункта (а) имеем: $S_{PMKN}=2S_{ABP}.$

При этом

$S_{ABP}=S_{ABN}-S_{APN}=\frac{AN\cdot BH_1}{2}-\frac{AN\cdot PT}{2}=\frac{9(12-\frac{108}{13})}{2}=\frac{432}{2\cdot 13}.$

Наконец, $S_{PMKN}=2S_{ABP}=\frac{432}{13}.$

Ответ: $\frac{432}{13}.$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Дима

2015-03-16 в 18:16

У Вас опечатка: Sabp=432/(13*2)

[ Ответить ]
- egeMax
  
  2015-03-16 в 20:21
  
  Дмитрий, спасибо!
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Поиск по сайту
Материалы для подготовки к ЕГЭ
С1 С3 С5 С6
Рубрики
- 01 Простейшие текст/задачи (2)
- 02 Читаем графики (1)
- 03 Геометрия, ч. I (11)
- 04 Теория вероятностей (2)
- 05 Простейшие уравнения (5)
- 06 Геометрия, ч. II (11)
- 07 Производная, ПО (4)
- 08 Стереометрия (11)
- 09 Вычисления (6)
- 10 «Прикладные» задачи (4)
- 11 Текстовые задачи (7)
- 12 Исследование функции (2)
- 13 (С1) Уравнения (72)
- 14 (С2) Стереометр. задачи (87)
- 15 (С3) Неравенства (82)
- 16 (С4) Планиметр. задачи (79)
- 17 (С5) Практич. задачи (66)
- 18 (С6) Параметры* (73)
- 19 (С7) Числа, их свойства (33)
- Видеоуроки (42)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (40)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (38)
- Переменка (7)
- Планиметрия (75)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (80)
- Стереометрия (52)
- Т/P A. Ларина (437)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (68)
- Тригонометрические выражения, уравнения и неравенства (45)
- Функции и графики (9)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы