Главная › 10 Графики функций › 10. Тригонометрическая функция

16 Сен 2022

Категория: 10 Графики функций

10. Тригонометрическая функция

Елена Репина 2022-09-16 2022-09-16

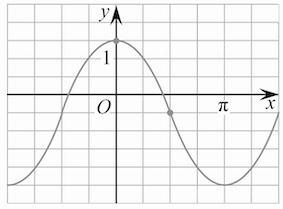
Задача 1. На рисунке изображён график функции $f(x)=acosx+b.$ Найдите $b.$

Решение: + показать

Задача 2. На рисунке изображён график функции $f(x)=acosx+b.$ Найдите $a.$

Решение: + показать

Задача 3. На рисунке изображён график функции $f(x)=atgx+b.$ Найдите $b.$

Решение: + показать

Задача 4. На рисунке изображён график функции $f(x)=atgx+b.$ Найдите $a.$

Решение: + показать

Задача 5. На рисунке изображён график функции $f(x)=asinx+b.$ Найдите $a.$

Решение: + показать

Задача 6. На рисунке изображён график функции $f(x)=acos(b\pi x+c)+d,$ где $a,b,c$ и $d$ – целые. Найдите $f(-\frac{8}{3}).$

Решение: + показать

Задача 7. На рисунке изображён график функции $f(x)=acos(\frac{\pi x}{b}+c)+d,$ где $a,b,c$ и $d$ – целые. Найдите $f(f(-\frac{20}{3})).$

Решение: + показать

Пройти тест

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы