Площади основных фигур. Набор формул
Эта таблица хороша для начального знакомства с темой “Площади фигур”.
Для более подготовленных учеников интересна будет расширенная таблица (!)
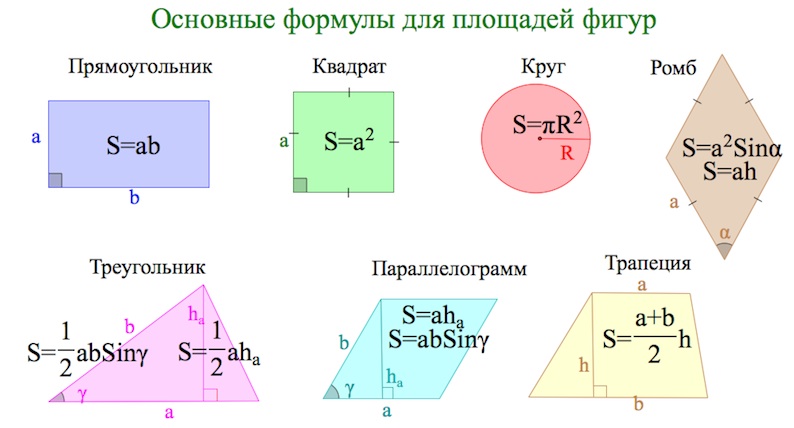

Площади основных фигур. Набор формул
Эта таблица хороша для начального знакомства с темой “Площади фигур”.
Для более подготовленных учеников интересна будет расширенная таблица (!)

хотелось бы по больше формул ;) например формулы периметра фигур
Собственно, что там расписывать-то? Только что формулу длины окружности? Для многоугольников же – знай себе – складывай длины всех сторон, да и все!
А по ссылке на этой странице проходили? Там еще больше формул площадей! ;)
Да, заглядывал, практически все формулы есть :)
Хотя можно добавить формулу площади правильного треугольника
И ещё, на одном сайте я видел вот такую формулу площади трапеции:
4r^2/SinA
Формула площади правильного треугольника здесь.
А формула [latexpage]$\frac{4r^2}{SinA}$ хороша, конечно, но встречается крайне редко. Во-первых, трапеция должны быть такой, чтоб в нее можно было вписать окружности, а во вторых, трапеция должна быть равнобедренной. Я бы не засоряла голову
«мысором»… Формула в раз выводится в случае необходимости…Ещё можно добавить формулы площади сектора, ведь всё это может встретиться на экзамене. Если в этой таблице будут абсолютно все формулы, ученику уже не придётся искать их где-то ещё…
Я своим ученикам говорю, чтоб на забивали себе голову формулой площади сектора. Ну вот зачем она?
Достаточно формулы площади круга, а дальше используется пропорция.
Но, сделать, конечно можно, для коллекционеров формул…
Ну вот, нужно как минимум объяснить как использовать пропорцию в данных задачах :)
Я например, посмотрев на формулу вычисления площади сектора, разобрался как составить пропорцию, то есть я не заучивал формулу, пытался разобраться в её сути, разобраться откуда эта формула берётся :)
Анатолий, многие бы позавидовали такому подходу! Так держать!
А ещё у меня такой вопрос: могу ли я утверждать что для ЛЮБОГО четырёхугольника действительна формула [latexpage]$(d_1\cdot d_2\cdot SinA)/2$ или $pr$ где r-радиус вписанной окружности, а p-полупериметр ?
Первая формула верна для любого 4-х-угольника (будь он прямоугольником, трапецией или вообще произвольным). А вот вторая – только для того 4-х-угольника, в который можно вписать окружность!
ну да, это я понимаю, если в 4-х-угольник нельзя вписать окружность откуда мы сможем взять радиус, который есть в формуле :D
:D :D :D