09. Задачи на работу

Пусть $x$ дет/час – скорость работы первого рабочего. Тогда $(x-3)$ дет/час – скорость второго рабочего.

Работа – это выполненные $130$ деталей.

Заполняем таблицу. Первые две колонки – согласно условию задачи, третью – автоматически (по формуле $t=\frac{A}{V}$).

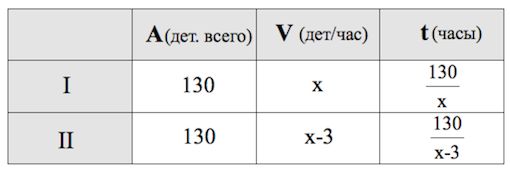
Поскольку первый рабочий выполняет  работу на $3$ часа быстрее, чем второй, то составим уравнение:

$\frac{130}{x}+3=\frac{130}{x-3};$

$130(x-3)+3x(x-3)=130x,\;x\neq0,\;x\neq3;$

$-130\cdot 3+3(x^2-3x)=0,\;x\neq0,\;x\neq3;$

$x^2-3x-130=0,\;x\neq0,\;x\neq3;$

$x=\frac{3\pm \sqrt{9+520}}{2};$

$x=\frac{3\pm 23}{2}.$

Откуда вытекает, что $x=13$ ($x=-10$ не подходит по условию задачи).

Ответ: $13.$ 

Пусть вторая труба пропускает $x$ литров воды в минуту. Тогда согласно условию первая труба пропускает $(x-4)$ л/мин.

Заполняем таблицу:

Время заполнения первой трубой резервуара на $4$ минуты дольше по сравнению со второй трубой, то есть $\frac{165}{x-4}$  больше  $\frac{165}{x}$ на $4.$

Поэтому

$\frac{165}{x-4}-\frac{165}{x}=4;$

$165x-165(x-4)=4x(x-4);$

$165\cdot 4=4x(x-4);$

$165=x^2-4x;$

$x^2-4x-165=0;$

$x=2\pm 13.$

Откуда следует, что $x=15.$ “Это производительность второй трубы.

А производительность первой тогда $15-4=11$ литров в минуту.

Ответ: $11.$ 

$\frac{156}{x-1}-\frac{143}{x}=2;$

$156x-143(x-1)=2x(x-1);$

$13x+143=2x^2-2x;$

$2x^2-15x-143=0;$

$x=\frac{15\pm \sqrt{225+1144}}{4};$

$x=\frac{15\pm 37}{4};$

 $x=13.$

Первая труба пропускает $x-1=13-1=12$ литров в минуту.

Ответ: $12.$ 

Так как двое рабочих выполняют работу (принимаем ее за 1) за $9$ дней, то их совместная производительность – $\frac{1}{9}$.

Пусть $x$ – дни, необходимые первому рабочему на выполнение всей работы.

Тогда скорость работы (производительность) первого рабочего – $\frac{1}{x}.$

За $5$ дней первый рабочий выполнит $\frac{1}{x}\cdot 5$ часть работы.

А поскольку и второй за $3$ дня выполнит такую же часть работы, то производительность второго рабочего – $\frac{5}{x}:3.$

Итак, скорость работы первого рабочего – $\frac{1}{x},$ второго – $\frac{5}{x}:3$, совместная скорость работы – $\frac{1}{9}$.

Тогда

$\frac{1}{x}+\frac{5}{3x}=\frac{1}{9};$

$\frac{8}{3x}=\frac{1}{9};$

$x=24.$

Ответ: $24.$

В этой задаче и не требуется вводить переменную. Задача  буквально выполняется по действиям.

Давайте проследим как заполнялась таблица.

1) В данном случае работа для нас абстрактна. Мы не можем ее измерить в страницах, деталях, литрах и т.п. В таких случаях обозначают работу за $1$ (можно было бы и за $x$ обозначить).

2) Производительность обоих рабочих – $\frac{1}{12}$ часть работы в час.

3) Раз первый рабочий работал $4$ часа с производительностью $\frac{1}{12}$, то он выполнил  $4\cdot \frac{1}{12}=\frac{1}{3}$ часть работы.

4) Оставшаяся часть работы – $\frac{2}{3}$.

5) При совместной работе производительности складываются. Поэтому вдвоем рабочие работают со скоростью $\frac{1}{12}+\frac{1}{12}=\frac{1}{6}$ часть работы в час.

6) Время работы I+II находим по формуле $t=\frac{A}{V}$. Получаем: $\frac{\frac{2}{3}}{\frac{1}{6}}=4$ часа.

Наконец, на выполнение всего заказа потребуется $4+4=8$ часов.

Ответ: $8.$

$\frac{1}{\frac{1}{36}+\frac{1}{12}}=\frac{1}{\frac{1}{9}}=9;$

Ответ: $9.$

Как заполнять первые три строки таблицы не должно вызывать у вас вопросы.

Далее, мы помним, что при совместной работе производительности складываются. Но при сложении величин из средних трех ячеек мы получим совместную производительность двух Игорей, двух Павлов и двух Владимиров, если так можно выразиться.

Именно поэтому производительность  Владимира, Игоря и Павла равна $\frac{\frac{1}{20}+\frac{1}{21}+\frac{1}{28}}{2}=\frac{\frac{21+20+15}{20\cdot 21}}{2}=\frac{1}{15}.$

Тогда мальчики покрасят забор, работая втроем за $\frac{1}{\frac{1}{15}}=15$ часов.

Ответ: $15.$

Сначала заполняем первую строку таблицы.

Далее третью, при этом переводим минуты в часы.

И, наконец, мы переходим ко второй строке. При этом, поскольку при совместной работе производительности складываются, то производительность  второй трубы есть разность производительностей совместной двух труб и производительности первой трубы.

Тогда вторая труба заполнит бассейн за $\frac{1}{\frac{1}{7\frac{11}{12}}-\frac{1}{38}}=\frac{1}{\frac{12}{95}-\frac{1}{38}}=\frac{1}{\frac{24-5}{19\cdot 5\cdot 2}}=\frac{19\cdot 5\cdot 2}{19}=10.$

Ответ: $10.$

Пусть в тесте $x$ вопросов. Скорость ответов на вопросы теста Пети – $10$ вопросов в час, Мити – $16$ вопросов в час.

$\frac{x}{10}$ (время ответа на весь тест Петей) на $117$ минут больше  $\frac{x}{16}$ (время ответа на весь тест Митей) согласно условию.

Не забываем перевести минуты в часы. $117$ минут $=\frac{117}{60}$ час. Поэтому

$\frac{x}{10}-\frac{x}{16}=\frac{117}{60};$

$\frac{3x}{80}=\frac{117}{60};$

$\frac{x}{8}=\frac{39}{6};$

$\frac{x}{4}=\frac{39}{3};$

$\frac{x}{4}=13;$

$x=52.$

Ответ: $52.$

Пусть $x$ – производительность одного рабочего, $t$ – время работы каждой бригады в новых составах.

$162x+21xt=198x+19xt;$

$36x=2xt;$

$t=18.$

Тогда заказы были выполнены каждой бригадой за $18+9=27$ дней.

Ответ: $27.$