Главная › 13 (С2) Стереометр. задачи › №16 (С2) из Тренировочной работы №86 А. Ларина

09 Окт 2014

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

№16 (С2) из Тренировочной работы №86 А. Ларина

Елена Репина 2014-10-09 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Задания 15, 17, 19, 20 из Тренировочного варианта № 86.

В прямую призму $ABCDA_1B_1C_1D_1$ , нижним основанием которой является ромб $ABCD$ , а $AA_1$ , $BB_1$ , $CC_1$ , $DD_1$ – боковые рёбра, вписан шар радиуса 1.

а) Постройте плоскость, проходящую через вершины $A$ , $B$ , $C_1$ .

б) Найдите площадь сечения призмы этой плоскостью, если известно, что $\angle BAD=\frac{\pi}{3}.$

Решение:

Сечение призмы плоскостью, проходящей через точки $A$ , $B$ , и $C_1$ – есть параллелограмм $AD_1C_1B$ .

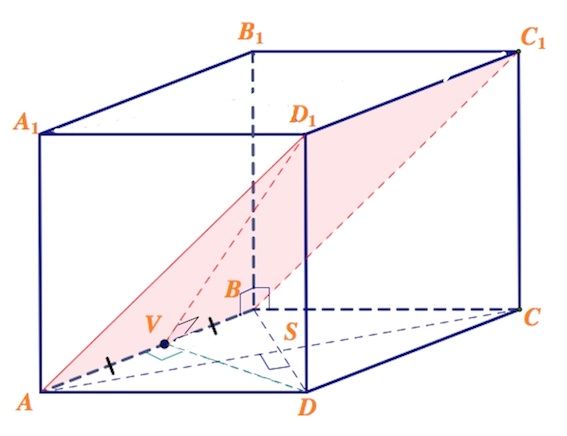
Действительно, поскольку мы знаем, что параллельные плоскости рассекаются третьей плоскостью по параллельным прямым, то плоскость $(ABC_1)$ пересекает плоскость грани $DCC_1D_1$ , параллельную $ABB_1A_1$ , по прямой $D_1C_1$ , параллельной $AB$ .

Поскольку шар вписан в призму, расстояния между всеми параллелыми гранями равны (и равны диаметру шара).

Опустим перпендикуляр $DV$ из т. $D$ к стороне $AB$ . По теореме о трех перпендикулярах $D_1V\perp AB$ .

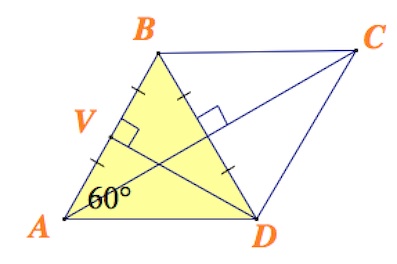
При этом $DV$ – именно расстояние между гранями $AA_1B_1B$ и $DD_1C_1C$ .

Итак, $DD_1=DV=2$ .

$\Delta VDD_1$ – прямоугольный с равными катетами. $VD_1=\sqrt2\cdot 2.$

Из равностороннего треугольнике $ABD$ с высотой $VD=2$ находим $AB:$

$sinA=\frac{VD}{AD};$

$\frac{\sqrt3}{2}=\frac{2}{AB};$

$AB=\frac{4}{\sqrt3}.$

Наконец, $S_{AD_1C_1B}=AB\cdot VD_1 =\frac{4\sqrt3}{3}\cdot 2\sqrt2=\frac{8\sqrt6}{3}$ .

Ответ: $\frac{8\sqrt6}{3}$ .

Автор: egeMax | комментария 2

Печать страницы

комментария 2

владимир

2015-08-09 в 15:21

В строке перед самым ответом умножение на 2 ошибочно, так как VD1 = 2 корня из 2. Видимо, опечатка (потому что результат умножения – верное число!)

[ Ответить ]
- egeMax
  
  2015-08-09 в 18:53
  
  Владимир, спасибо! корень из 2-х не пропечатался… Исправлено.
  
  [ Ответить ]

№16 (С2) из Тренировочной работы №86 А. Ларина

Добавить комментарий Отменить ответ