12 Сен 2013

Категория: 08 Стереометрия

08. Призма

Елена Репина 2013-09-12 2021-07-20

Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна $15,$ а площадь поверхности равна $930.$

4b77feb149b13ef53686a64f18a07141

Решение: + показать

Задача 2. В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ известно, что $DB_1=2C_1D_1.$ Найдите угол между диагоналями $BD_1$ и $AC_1.$ Ответ дайте в градусах.

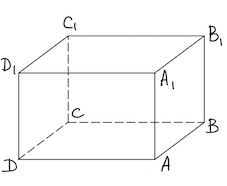
Решение: + показать

Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами $5$ и $7,$ боковое ребро равно $4.$ Найдите объем призмы.

Решение: + показать

Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами $6$ и $8,$ высота призмы равна $10.$ Найдите площадь ее поверхности.

Решение: + показать

Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами $5$ и $12.$ Площадь ее поверхности равна $120$ . Найдите высоту призмы.

Решение: + показать

Задача 6. Площадь поверхности правильной треугольной призмы равна $10.$ Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?

Решение: + показать

Задача 7. В правильной треугольной призме $ABCA_1B_1C_1$ , все ребра которой равны $1,$ найдите угол между прямыми $AA_1$ и $BC_1$ . Ответ дайте в градусах.

Решение: + показать

Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $25$ и $60,$ и боковым ребром, равным $25.$

389087dae8e7dd88c8250467ac3c2d76

Решение: + показать

Задача 9. Гранью параллелепипеда является ромб со стороной $4$ и острым углом $60^{\circ}.$ Одно из ребер параллелепипеда составляет с этой гранью угол в $60^{\circ}$ и равно $5.$ Найдите объем параллелепипеда.

Решение: + показать

Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна $3,$ а высота — $10.$

Решение: + показать

Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны $8,$ а боковые ребра равны $\sqrt{0,75}.$

Решение: + показать

Задача 12. В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ все ребра равны $14\sqrt5$ . Найдите расстояние между точками $C$ и $F_1$ .

Решение: + показать

Задача 13. В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ все ребра равны $5.$ Найдите угол $E_1EC_1$ . Ответ дайте в градусах.

Решение: + показать

Задача 14. В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ , все ребра которой равны $1,$ найдите угол между прямыми $AB$ и $C_1D_1$ . Ответ дайте в градусах.

Решение: + показать

Задача 15. В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ все ребра равны $19.$ Найдите тангенс угла $AD_1D.$

Решение: + показать

Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили $1300$ см $^3$ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки $25$ см до отметки $28$ см. Найдите объем детали. Ответ выразите в см $^3.$

Решение: + показать

Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает $18$ см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в $3$ раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Решение: + показать

Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен $19,5.$ Найдите объем исходной призмы.

Решение: + показать

Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами $8,$ а боковые ребра равны $4\sqrt3$ и наклонены к плоскости основания под углом $30^{\circ}.$

d208102cf7eb1a42bdbb4620fb536be6

Решение: + показать

Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно $16$ и отстоит от других боковых ребер на $9$ и $12.$ Найдите площадь боковой поверхности этой призмы.

Решение: + показать

Задача 23. В правильной треугольной призме $ABCA_1B_1C_1$ стороны оснований равны $2\sqrt3,$ боковые рёбра равны $5.$ Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер $AB$ , и $A_1B_1$ и точку $C.$

Решение: + показать

Задача 24. В правильной треугольной призме $ABCA_1B_1C_1$ стороны оснований равны $6,$ боковые рёбра равны $2.$ Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер $AB,$ $AC,$ $A_1B_1$ и $A_1C_1.$

Решение: + показать

Задача 25. Объём куба $ABCDA_1B_1C_1D_1$ равен $160.$ Построено сечение $EFF_1E_1,$ проходящее через середины рёбер $BC,CD$ и $C_1D_1$ и параллельное ребру $CC_1.$ Найдите объём треугольной призмы $CEFC_1E_1F_1.$

Решение: + показать

Задача 26. Найдите объем многогранника, вершинами которого являются точки $A,B,C,A_1,C_1$ правильной треугольной призмы $ABCA_1B_1C_1,$ площадь основания которой равна $3,$ а боковое ребро равно $7.$

Решение: + показать

Задача 27. Найдите объем многогранника, вершинами которого являются точки $A,B,A_1,C_1$ правильной треугольной призмы $ABCA_1B_1C_1$ площадь основания которой равна $4,$ а боковое ребро равно $6.$

Решение: + показать

Задача 28. Найдите объем многогранника, вершинами которого являются точки $B,C,D,B_1,C_1,D_1$ правильной шестиугольной призмы $ABCDEFA_1B_1C_1D_1E_1F_1,$ площадь основания которой равна $3,$ а боковое ребро равно $5.$

Решение: + показать

Задача 29. Найдите объём многогранника, вершинами которого являются точки $A,B,C,D,E,F,D_1$ правильной шестиугольной призмы $ABCDEFA_1B_1C_1D_1E_1F_1,$ площадь основания которой равна $5,$ а боковое ребро равно $9.$

Решение: + показать

Вы можете пройти тест «Призма»

Автор: egeMax | комментариев 13

Печать страницы

комментариев 13

Анатолий Шевелев

2014-01-16 в 10:03

Объясните пожалуйста 6-ю задачу… когда я прочитал задачу я сразу подумал что нужно найти площадь треугольника А1D1K, а оказалось что требуется найти прямоугольник А1D1МK…

[ Ответить ]
- egeMax
  
  2014-01-16 в 10:10
  
  Сечение – это все точки геометрического тела, которые лежат на секущей плоскости. $A_1D_1K$ – это только часть сечения!
  Точка М также попадает в плоскость $(A_1D_1K)$ .
  
  [ Ответить ]
  - Анатолий Шевелев
    
    2014-01-16 в 10:23
    
    хорошо, буду знать, спасибо :)
    
    [ Ответить ]
Анатолий Шевелев

2014-01-16 в 11:18

Вот ещё вопрос, я не совсем понял разницу между диагональной плоскостью, диагональным сечением и перпендикулярным сечением…
Там в статье есть рисунок но там не обозначено где какое сечение изображено…

[ Ответить ]
- egeMax
  
  2014-01-16 в 11:31
  
  Диагональная плоскость – сделайте акцент на плоскость. Диагональная плоскость (плоскость, проходящая через боковое ребро призмы и диагональ основания) содержит диагональное сечение (многоугольник).
  
  Перпендикулярное же сечения – другая история. Прежде проводится плоскость, перпендикулярная боковому ребру. Тогда эта плоскость пересечет призму по некоторому многоульнику – его и называем перпендикулярным сечением.
  
  [ Ответить ]
  - Анатолий Шевелев
    
    2014-01-16 в 11:37
    
    То есть, по сути, на практике, между диагонадьной плоскостью и диагональным сечением разницы нет, на процесс решения это не повлияет? )
    
    [ Ответить ]
    - egeMax
      
      2014-01-16 в 11:45
      
      Город Москва – часть территории России.
      Территория Москвы ≠ территории России.
      Одно множество вбирает в себя другое…
      Так и диагональная плоскость (бесконечна) вбирает в себя диагональное сечение.
      Вы не сможете, к примеру, найти площадь диагональной плоскости, но найти площадь сечения (многоугольника) можно… ;)
      
      [ Ответить ]
Анатолий Шевелев

2014-01-16 в 11:54

“Напомним, что правильная треугольная призма – прямая призма, у которой в основании – квадрат.” – неужели действительно квадрат? :D

[ Ответить ]
- egeMax
  
  2014-01-16 в 12:06
  
  :D :D :D
  
  [ Ответить ]
Мариана

2014-12-08 в 22:39

в задаче 7 ответ неверный. По определению угол между прямыми лежит в пределах от 0 до 90 градусов, поэтому надо брать не тупой, а смежный с ним острый.Ответ: 60.

[ Ответить ]
- egeMax
  
  2014-12-09 в 00:54
  
  Мариана, конечно. Спасибо большое! Спешка…
  
  [ Ответить ]
лена

2016-10-24 в 00:59

Здравствуйте!!! не понятно почему в 7 задаче ответ 60, а не 120?

[ Ответить ]
- egeMax
  
  2016-10-24 в 07:02
  
  Потому что угол между двумя пересекающимися прямыми – это мера меньшего из четырех углов, образованных этими прямыми.
  
  [ Ответить ]

08. Призма

Добавить комментарий Отменить ответ