Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

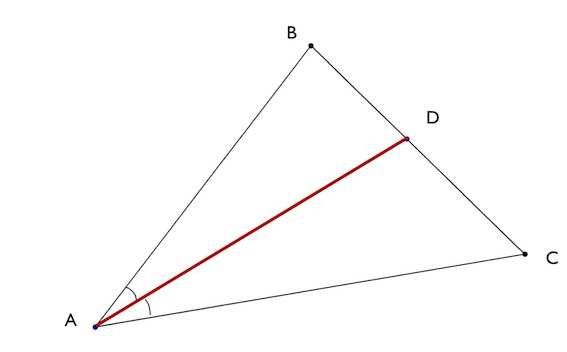
Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса  угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ($\frac{{AB}}{{AC}} = \frac{{BD}}{{CD}}$)

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

$l_c = {\sqrt{ab(a+b+c)(a+b-c)}\over{a+b}}$ (доказательство формулы – здесь)
$l_c = \sqrt{ab-a_lb_l}$, где
$l_c$ — длина биссектрисы, проведённой к стороне $c$,
$a, b, c$ — стороны треугольника против вершин $A, B, C$ соответственно,
$a_l, b_l$ — длины отрезков, на которые биссектриса $l_c$ делит сторону $c$,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы