Главная › 14 (С3) Неравенства › C3 (№17). Логарифмическое неравенство. Часть 2 (метод рационализации)

08 Июн 2013

Категория: 14 (С3) НеравенстваИррациональные выражения, уравнения и неравенстваЛогарифмыМетод рационализации

C3 (№17). Логарифмическое неравенство. Часть 2 (метод рационализации)

Елена Репина 2013-06-08 2016-04-15

Продолжение

Начало – здесь.
Решим неравенство $\frac{1-\sqrt{1-4log^2_8x}}{log_8x}<2$ методом рационализации.

Как и в предыдущем случае сделаем замену $m=log_8x$ . Перенесем 2 влево и приведем к общему знаменателю:

$\frac{1-\sqrt{1-4m^2}-2m}{m}<0$ .

Заметим, $\sqrt{(1-2m)^2}=|1-2m|$ , но если $1-2m\geq 0$ , то $\sqrt{(1-2m)^2}=1-2m$ и мы смогли применить рационализацию

2wertd

Поэтому рассмотрим два случая:

1) $1-2m< 0$ , то есть $m>\frac{1}{2}$ . В этом случае, так как $1-4m^2$ должно быть неотрицательным, то и $1+2m\leq 0$ , то есть $m\leq-\frac{1}{2}$ .

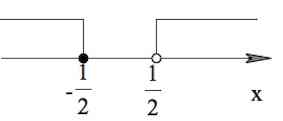
Выходит, такой случай невозможен. Очень хорошо, – будем применять рационализацию.

2) $1-2m\geq 0$ .

Исходное неравенство можно переписать так

$\frac{\sqrt{(1-2m)^2}-\sqrt{1-4m^2}}{m}<0$ .

Согласно методу рационализации данное неравенство равносильно следующему:

$\frac{1-4m+4m^2-(1-4m^2)}{m}<0$ при условии, что $1-4m^2\geq 0$ .

Ну или что тоже самое, что и $m(1-4m+4m^2-1+4m^2)<0,\;1-4m^2\geq 0$ .

Итак, перед нами система:

$\begin{cases} & m(-4m+8m^2)<0, & & 1-4m^2\geq 0; \end{cases}$

Откуда

$\begin{cases} & 4m^2(2m-1)<0, & & (1-2m)(1+2m)\geq 0; \end{cases}$

Решение первого неравенства системы:

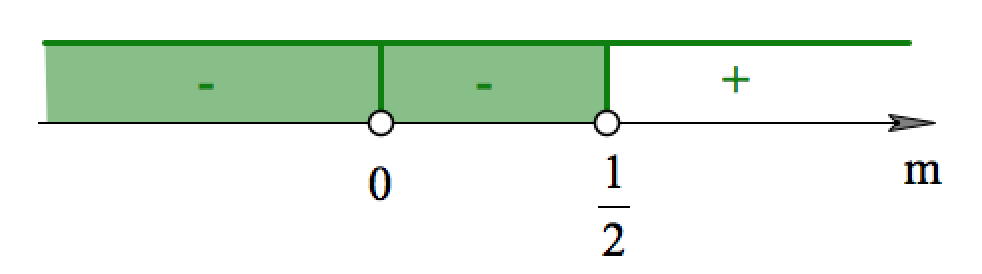
Снимок экрана 2013-06-09 в 10.20.33

Обратите внимание, что при переходе через точку «0», – не произошла смена знаков, так как «0» – корень четной кратности.

На этой же координатной оси отмечаем решение второго неравенства системы:

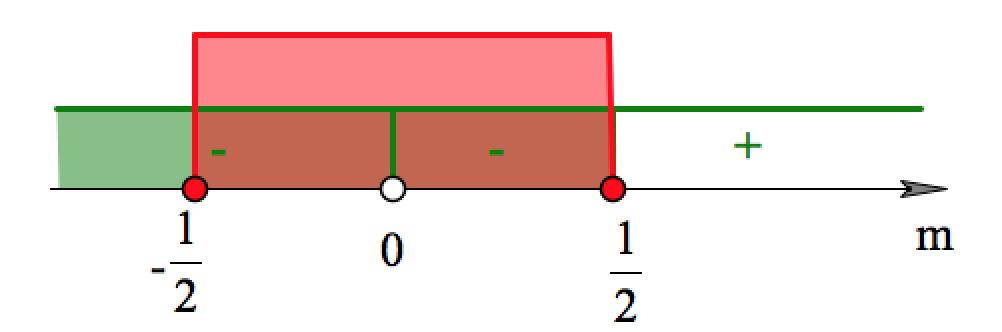
Снимок экрана 2013-06-10 в 9.44.55

В пересечении имеем: $m\in [-\frac{1}{2};0)\cup(0;\frac{1}{2})$ .

Осталось лишь сделать обратную замену:

$-0.5\leq log_8x<0$ или $0<log_8x<0.5$

$8^{-0.5}\leq x<8^0$ или $8^0<x<8^{0.5}$

$\frac{\sqrt2}{4}\leq x<1$ или $1<x<2\sqrt2$ .

Ответ: $[\frac{\sqrt2}{4}; 1)\cup(1;2\sqrt2)$

Вы заметили, что мы решили быстрее неравенство (использую метод рационализации) по сравнению с предыдущим случаем?
Тогда «вооружайтесь» этим методом, и на экзамене у вас будет больше времени на обдумывание остальных заданий.

Третий способ решения (через обобщеннный метод интервалов) смотрите здесь.

Автор: egeMax | Нет комментариев | Метки: метод рационализации

Печать страницы

C3 (№17). Логарифмическое неравенство. Часть 2 (метод рационализации)

Продолжение

Добавить комментарий Отменить ответ