C3 Т/Р №66 Ларина

Решите систему неравенств:

$\begin{cases}log_2(5-x)(2-x)>log_4(x-2)^2,\\\frac{2^x-2^{2-x}-3}{2^x-2}\geq 0;&\end{cases}$

Решение:

Рассмотрим первое неравенство системы:

$log_2(5-x)(2-x)>log_4(x-2)^2;$

Заметим, что $log_4(x-2)^2=2log_{2^2}|x-2|=log_2|x-2|.$

Тогда неравенство

$log_2(5-x)(2-x)>log_2|x-2|$

будем решать путем рассмотрения двух случаев: $x>2$ и $x<2.$

Выходим на совокупность двух систем:

$\left[\begin{array}{rcl}\begin{cases}x>2,\\log_2(x-5)(x-2)>log_2(x-2);\end{cases}\\\begin{cases}x<2,\\log_2(5-x)(2-x)>log_2(2-x);\end{cases}\\\end{array}\right.$

Обратите внимание, мы не случайно указали во второй строке первой системы $log_2(x-5)(x-2)$ вместо $log_2(5-x)(2-x)$. Нам предстоит «расклейка» логарифмов, мы ведем подготовительную работу.

$\left[\begin{array}{rcl}\begin{cases}x>2,\\log_2(x-5)+log_2(x-2)>log_2(x-2);\end{cases}\\\begin{cases}x<2,\\log_2(5-x)+log_2(2-x)>log_2(2-x);\end{cases}\end{array}\\\right.$

$\left[\begin{array}{rcl}\begin{cases}x>2,\\log_2(x-5)>0;\end{cases}\\\begin{cases}x<2,\\log_2(5-x)>0;\end{cases}\end{array}\\\right.$

$\left[\begin{array}{rcl}\begin{cases}x>2,\\x-5>1;\end{cases}\\\begin{cases}x<2,\\5-x>1;\end{cases}\end{array}\\\right.$

$\left[\begin{array}{rcl}\begin{cases}x>2,\\x>6;\end{cases}\\\begin{cases}x<2,\\x<4;\end{cases}\end{array}\\\right.$

$\left[\begin{array}{rcl}x>6,\\x<2;\end{array}\right.$

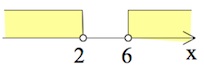
Рассмотрим второе неравенство системы:

$\frac{2^x-2^{2-x}-3}{2^x-2}\geq 0;$

$\frac{2^x-4\cdot 2^{-x}-3}{2^x-2}\geq 0;$

Так как $2^x>0$ по определению, то домножим обе части неравенства на $2^x:$

$\frac{(2^x)^2-4\cdot 2^{-x}\cdot 2^x-3\cdot 2^x}{2^x-2}\geq 0;$

$\frac{(2^x)^2-3\cdot 2^x-4}{2^x-2}\geq 0;$

В числителе – квадратный трехчлен относительно $2^x.$ Найдем его корни через дискриминант и разобьем его на множители:

$\frac{(2^x-4)(2^x+1)}{2^x-2}\geq 0;$

Имеем:

$\left[\begin{array}{rcl}2^x<2,\\2^x\geq 4;\end{array}\right.$

$\left[\begin{array}{rcl}x<1,\\x\geq 2;\end{array}\right.$

Наконец, пересекаем решения неравенств исходной системы:

Ответ: $(-\infty;1)\cup(6;+\infty).$

Смотрите также C2(№16), C4(№18) Тренировочной работы №66