C4, пересекающиеся окружности с общей касательной

С4 Тренировочной работы №60 А. Ларина

Смотрите также С1(№15) и С3(№17) Т/Р №60.

В 2013 году расширена форма заданий С4. Теперь в задании С4 может встретиться пункт на доказательство какого-либо факта. Рассмотрим одну из задач, так скажем, нового формата.

Продолжение общей хорды АВ двух пересекающихся окружностей радиусов 8 и 2 пересекает их общую касательную в точке С, точка А лежит между В и С, а М и N – точки касания.
а) Докажите, что отношение расстояний от точки С до прямых АМ и AN равно 1:2;
б) Найдите радиус окружности, проходящей через точки А, М и N.

Решение:

a)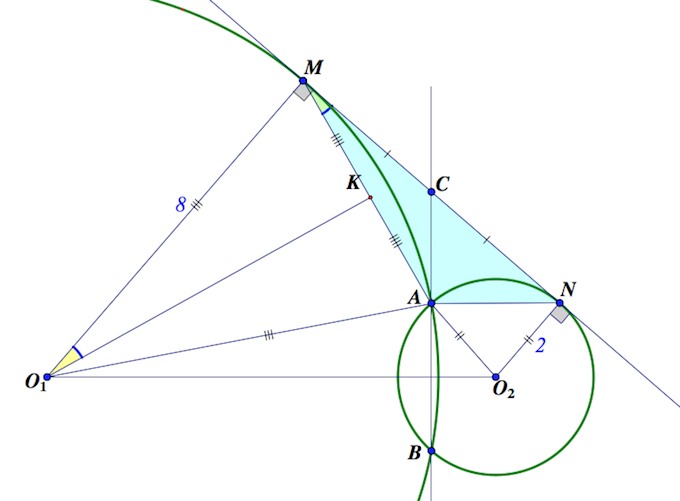 

По свойству касательной и секущей, проведенных  к окружности из одной точки: $CM^2=CA\cdot CB$ и $CN^2=CA\cdot CB.$ Стало быть, $CM=CN.$

Значит, $AC$ – медиана треугольника $AMN$. А мы знаем, что медиана делит треугольник на два равновеликих треугольника (в силу совпадения высот, проведенным к равным сторонам $CN,\;CM$). Тогда $\rho_1\cdot AM=\rho_2\cdot AN,$ где $\rho_1 $ – расстояние от точки $C$ до стороны $AM$, $\rho_2$ – расстояние от точки $C$ до стороны $AN$.

Докажем, что $AM=2AN$, – это и будет означать, что $\rho_1:\rho_2=1:2.$

Пусть $K$ – середина основания $AM$ равнобедренного треугольника $AMO_1,$ где $O_1$ – центр большей окружности.

Тогда из прямоугольного треугольника $O_1MK$  $sinMO_1K=\frac{MK}{8}=\frac{AM}{16}.$

Заметим, что $\angle MO_1K=\angle AMN$, так как оба угла составляют в сумме $90^{\circ}$ с одним и тем же углом $O_1MK$.

Тогда  и $sinAMN=\frac{AM}{16}.$

Рассуждая аналогичным образом, приходим к тому, что и $sinANM=\frac{AN}{4}.$

С другой стороны, по т. Синусов из треугольника $AMN$

$\frac{AM}{sinANM}=\frac{AN}{sinAMN}=2R$,

где $R$ – радиус окружности, описанной около треугольника $AMN$.

Значит, $\frac{AM}{\frac{AN}{4}}=\frac{AN}{\frac{AM}{16}}$, откуда $\frac{AM}{AN}=\frac{4AN}{AM}$ и, наконец, $AM=2AN.$

б) Как мы уже говорили, $\frac{AM}{sinANM}=2R$, то есть $\frac{AM}{\frac{AM}{8}}=2R$, откуда $R=4.$

Ответ: 4.