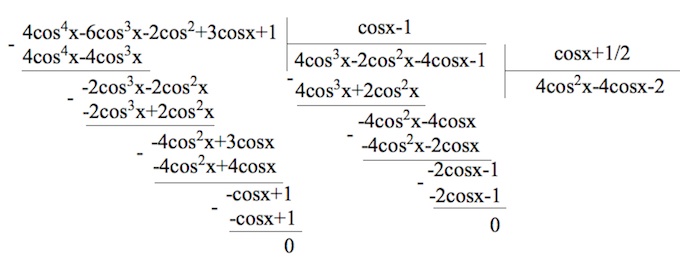Подготовка к ЕГЭ по математике

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение $tg(1-x)+tg2x=0.$

а) Решите уравнение.

б) Найдите его корни на отрезке $[2;8].$
Читать далее

Смотрите также  №16, №17, №18, №19, №20.

Читать далее

Смотрите также №16, №17, №18, №19, №20.

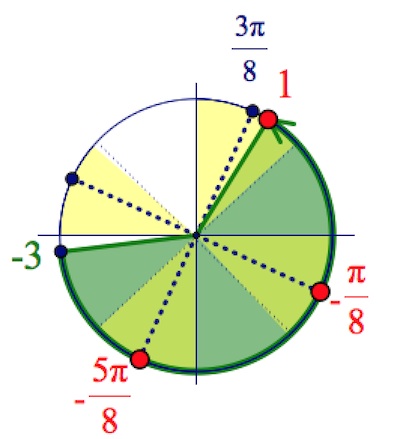
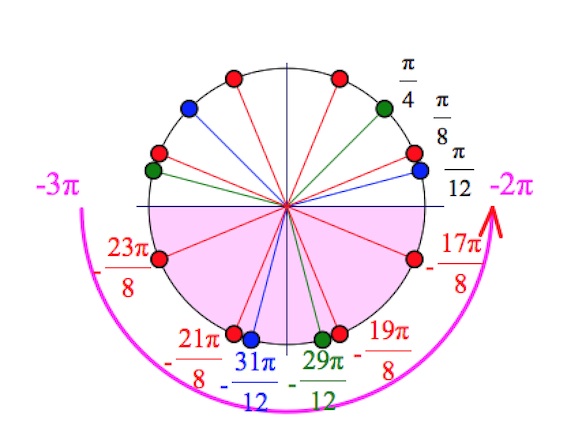
Дано уравнение $(1-cos2x)(ctgx-\sqrt3)=3sinx-\sqrt3cosx.$

а) Решите уравнение;

б) Найдите его корни, принадлежащие промежутку $[-2\pi;-\frac{\pi}{2}].$ Читать далее

Смотрите также  №16, №17, №18, №19, №20.

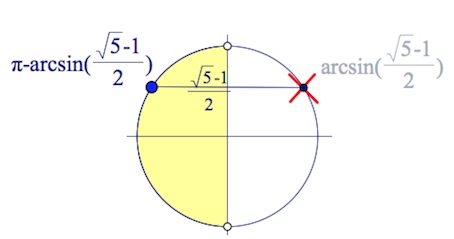
Дано уравнение $\frac{2}{4^{sin^2x}}=\frac{4^{sinx}}{2^{2cosx}}.$

a) Решите уравнение;

б) Найдите его корни, принадлежащие промежутку $[\frac{3\pi}{2};3\pi].$ Читать далее

Смотрите также №16, №17, №18, №19, №20.
Дано уравнение

$cos4x-6cos2xcosx-4sin^2x+5=0$.

а) Решите уравнение.
б) Найдите его корни, принадлежащие промежутку $[\pi;\frac{5\pi}{2}].$ Читать далее

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение $log_{-cosx}2\cdot log_2(sinx)=2$

а) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие отрезку $[\frac{17\pi}{6};\frac{19\pi}{4}]$. Читать далее

Смотрите также №16, №17, №18, №19, №20

Решите уравнение: $\sqrt{3-x^2-2x}\cdot log_2(-sin4x)=0.$ Читать далее

Смотрите также №16, №17, №18, №19, №20

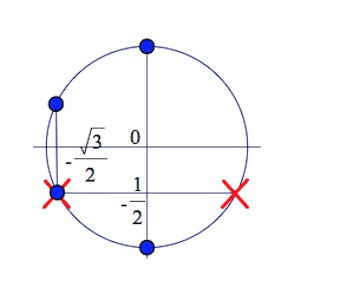
Дано уравнение $\frac{2cos^2x+\sqrt3cosx}{2sinx+1}=0.$

а) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие промежутку $[2\pi;\frac{7\pi}{2}).$ Читать далее

Дано уравнение $sin7x-sinx=\sqrt2cos4x.$

а) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие отрезку $[-3\pi;-2\pi].$ Читать далее

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение

$25^{cos(\frac{3\pi}{2}+x)}=5^{1-cos2x}.$

а) Решите уравнение.

б) Укажите корни этого уравнения, принадлежащие интервалу

$(-5\pi;-\frac{3\pi}{2}).$ Читать далее

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение

$2sin^2x+cos4x=0$

a) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие отрезку $[\frac{5\pi}{2};3\pi].$

Читать далее

Смотрите также №16, №17, №18, №19, №20

Дано уравнение

$\frac{|cosx|}{cosx}+2=2sinx$

а) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие отрезку $[8,5;14,5].$
Читать далее

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение

$\sqrt{sin2x}=\sqrt{\sqrt3cosx}.$

a) Решите уравнение;

б) Найдите его корни, принадлежащие отрезку $[4,5;7,5].$
Читать далее