Подготовка к ЕГЭ по математике

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №204 А. Ларина.

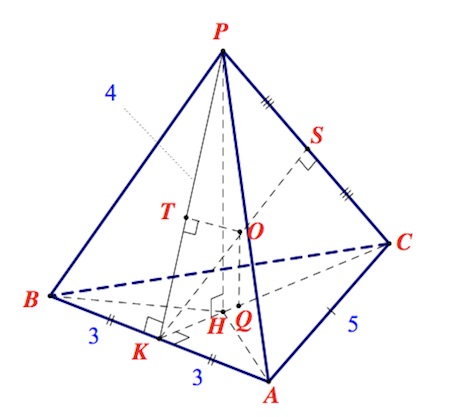
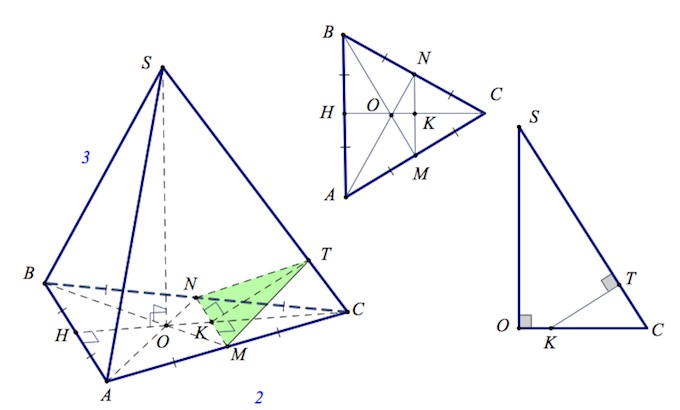
14. В основании пирамиды $SABC$ лежит равнобедренный треугольник $ABC$, в котором $AB=4,\angle BAC=120^{\circ}$. Известно, что боковая грань $SBC$ перпендикулярна

основанию $ABC$,  $SB=SC$, а высота пирамиды, проведенная из точки $S$, равна $2\sqrt{11}$ . На ребрах $SB$ и $SC$ отмечены соответственно точки $K$ и $P$ так, что $BK:SK=CP=SP=1:3.$
а) Докажите, что сечением пирамиды плоскостью $APK$ является прямоугольный треугольник.

б) Найдите объем меньшей части пирамиды, на которые её делит плоскость $APK$.

Читать далее

Смотрите также №13; №15; №16; №17; №18  Тренировочной работы №203 А. Ларина.

14. Дана прямая призма $ABCA_1B_1C_1.$

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №202 А. Ларина.

14. В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=2,AD=1, AA_1=3.$ Точка $K$ лежит на ребре $CC_1$ так, что $CK:C_1K=5:4.$
а) Докажите, что прямые $DB_1$  и $D_1K$ перпендикулярны.

б) Найдите расстояние от точки $D_1$ до плоскости $KA_1D$.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №197 А. Ларина.

14. В конусе с вершиной в точке $P$ высота равна $1$, а образующая равна $2$. В основании конуса провели диаметр $CD$ и перпендикулярную ему хорду $AB$. Известно, что хорда

$AB$ удалена от центра основания на расстояние, равное $1$.

а) Докажите, что треугольник $PAB$ прямоугольный.
б) Найдите сумму объемов пирамид $CAPB$ и $DAPB$.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №196 А. Ларина.

14. В основании пирамиды $PABC$ лежит равнобедренный треугольник $ABC$ $(AC=BC).$ Все боковые ребра пирамиды попарно равны. Точка $K$ – середина $AB$. В эту пирамиду вписана сфера.

а) Докажите, что точка касания сферы с гранью $APB$ лежит на прямой $PK$.

б) Найдите радиус сферы, если известно, что $AB=6,BC=5,KP=4$.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №194 А. Ларина.

14. В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ $AB=BC=8,AA_1=6$.

Через точки $A$ и $C$ перпендикулярно $BD_1$ проведена плоскость Ω.
а) Докажите, что плоскость Ω пересекает ребро $B_1C_1$ в такой точке $M$, что $MB_1:MC_1=7:9.$

б) Найдите угол между плоскостями Ω и $ACC_1$.

Читать далее

Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №194 А. Ларина.

16. Точки $M$ и $P$ – середины сторон $BC$ и $AD$ выпуклого четырехугольника $ABCD$. Диагональ $AC$ проходит через середину отрезка $MP$.

а) Докажите, что площади треугольников $ABC$ и $ACD$ равны.
б) Найдите радиус окружности, вписанной в треугольник $ABM$, если известно, что $AB=12,BC=10,$ а площадь четырехугольника $AMCP$ равна $60$.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №184 А. Ларина 

14. В правильной треугольной пирамиде $SABC$, точки $P$, $Q$, $R$ лежат на боковых ребрах $AS$, $CS$ и $BS$, причем $\frac{SP}{AP}=\frac{CQ}{QS}=\frac{SR}{RB}=2.$

а) Доказать, что объемы пирамид $SPRQ$ и $SABC$ относятся как $4:27$.

б) Найти объем пирамиды $CPQR$, если $AB=2$ и $SA=3$.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №183 А. Ларина 

14. В правильной треугольной пирамиде $SABC$ ребро основания $AB$ равно $2$, а боковое ребро $AS$ равно $\sqrt5.$ Через точки $S$, $A$ и середину стороны $BC$ – точку $K$ проведено сечение.

Найдите

а) Площадь сечения.

б) Косинус угла между сечением и плоскостью $ABC$. 

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №181 А. Ларина 

14. В правильной пирамиде $SABC$ ребра $AB=2$, $SC=3$. Через среднюю линию $MN$ треугольника $ABC$, параллельную $AB$, проведено сечение минимальной площади пирамиды $SABC$, пересекающее ребро $SC.$
А) Докажите, что это сечение перпендикулярно ребру $SC$.

Б) Найдите площадь этого сечения.

Читать далее

Смотрите также №13; №15; №16; №17; №18; №19  Тренировочной работы №176 А. Ларина 

14. В правильной четырехугольной пирамиде $PABCD$ сторона основания равна $20$, а высота пирамиды равна $11,25$. Через ребро $AB$ под углом $\beta $ к плоскости $ABC$ проведена плоскость α. Известно, что $tg\beta =\frac{3}{4}.$
а) Докажите, что плоскость α делит ребро $PC$ в отношении $1:4$, считая от точки $P$.

б) Найдите площадь сечения пирамиды плоскостью α.

Читать далее

Смотрите также  №13; №15; №16; №17; №18  Тренировочной работы №173 А. Ларина

14. В основании приямой призмы $ABCDA_1B_1C_1D_1$ лежит трапеция $ABCD$ с основаниями $BC$ и $AD$. Точка $K$ – середина ребра $BB_1$. Плоскость $\alpha $ проходит через середины ребер $AB$ и $BB_1$ параллельно прямой $B_1D$.
А) Докажите, что сечением призмы плоскостью $\alpha $ является равнобедренная трапеция.

Б) Найдите объем большей части призмы, на которые ее разбивает плоскость $\alpha $, если известно, что $BC=7,AD=25,AB=15,BB_1=8.$

Читать далее

 Смотрите также  №13; №15; №16; №17; №18; №19  Тренировочной работы №171 А. Ларина

14. В правильной шестиугольной призме $ABCDEFA_1B_1C_1D_1E_1F_1$ на ребре $CC_1$

отмечена точка $M$ так, что $CM:C_1M=1:3$. Плоскость $AEM$ пересекает ребро $BB_1$ в точке $K$.

а) Докажите, что $BK:B_1K=1:5$.
б) Найдите площадь сечения призмы плоскостью $AEM$, если $AB=3,CC_1=8$.

Читать далее