Планиметрия | Подготовка к ЕГЭ по математике

Архив по категории: Планиметрия

14 Июл 2020

Задание №16. Реальный ЕГЭ от 10 июля 2020

Елена Репина 2020-07-14 2020-07-14

Разбор заданий №13; №14; №15; №17; №18; №19 (в процессе оформления)

16. На сторонах $AB, BC$ и $AC$ треугольника $ABC$ отмечены точки $C_1$ , $A_1$ и $B_1$ соответственно, причём $AC_1:C_1B= 8: 3$ , $BA_1:A_1C = 1: 2$ , $CB_1:B_1A = 3 ∶ 1$ .
Отрезки $BB_1$ и $CC_1$ пересекаются в точке $D$ .
а) Докажите, что $ADA_1B_1$ — параллелограмм.
б) Найдите $CD$ , если отрезки $AD$ и $BC$ перпендикулярны, $AC=28, BC = 18$ .

Автор: egeMax | комментария 2

Категория: 16 (С5) Планиметр. задачиЕГЭ (диагностич. работы)Планиметрия

25 Сен 2019

№16 Тренировочного варианта 280 А. Ларина

Елена Репина 2019-09-25 2019-09-26

Смотрите также №14 Т/Р №280

16. В треугольнике $ABC$ провели высоты $AA_1$ и $BB_1$ . Окружность, описанная вокруг треугольника $ANA_1$ , где точка $N$ – середина стороны $AB$ , пересекла прямую $A_1B_1$ в точке $K$ .
а) Докажите, что прямая $AK$ касается окружности, описанной около треугольника $ABC$ .
б) Найдите отношение площадей четырехугольника $ABA_1B_1$ и треугольника $CA_1B_1$ , если $\angle ABC=45^{\circ}$ , $AB_1=BN=1$ .

Решение:

Ответ: $7+4\sqrt3.$

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

06 Сен 2019

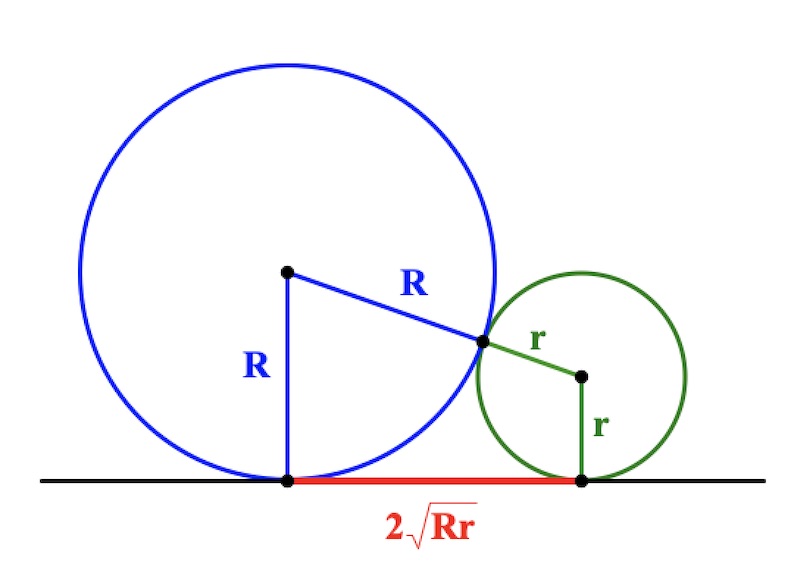
Теорема о длине внешней общей касательной к окружностям

Елена Репина 2019-09-06 2019-09-08

Данное утверждение может быть очень полезно при решении задач на внешне касающиеся окружности.

Теорема Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов. Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияСправочные материалы

01 Июн 2015

Задание №18 Т/Р №120 А. Ларина

Елена Репина 2015-06-01 2016-09-07

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

Окружности $\omega 1$ с центром $O_1$ и окружность $\omega 2$ с центром $O_2$ касаются внешним образом. Из точки $O_1$ к $\omega 2$ проведена касательная $O_1A$ , а из точки $O_2$ к $\omega 1$ проведена касательная $O_2B$ ( $A$ и $B$ – точки касания).
a) Докажите, что углы $O_1AB$ и $O_1O_2B$ равны.
б) Найдите площадь четырехугольника $O_1O_2AB$ , если известно, что точки $A$ и $B$ лежат по одну сторону от прямой $O_1O_2$ , а радиусы окружностей равны соответственно $2$ и $3$ . Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

28 Май 2015

Задание №18 Т/Р №119 А. Ларина

Елена Репина 2015-05-28 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.
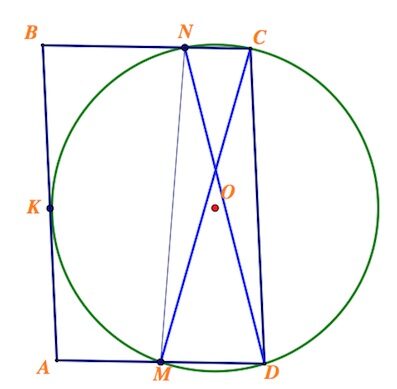
В прямоугольном треугольнике $ABC$ $\angle C=90^{\circ}$ проведены медианы $AM$ и $BK$ . Известно, что около четырехугольника $ABMK$ можно описать окружность.
а) Докажите, что $CK=CM$ .
б) Пусть $AB=2$ . Найдите радиус окружности, описанной около четырехугольника $ABMK$ .

Автор: egeMax | комментариев 5

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

21 Май 2015

Задание №18 Т/Р №118 А. Ларина

Елена Репина 2015-05-21 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

Автор: egeMax | комментариев 7

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

07 Май 2015

Задание №18 Т/Р №116 А. Ларина

Елена Репина 2015-05-07 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

В треугольнике $ABC$ проведена биссектриса $CM$ . Касательная к описанной окружности треугольника $ABC$ , проходящая через точку $C$ , пересекает прямую $AB$ в точке $P$ .

а) Докажите, что $BC:AC=CP:AP$ .
б) Найдите длину отрезка $CP$ , если известно, что $AM=5, BM=4.$

Автор: egeMax | комментариев 6

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

23 Апр 2015

Задание №18 Т/Р №114 А. Ларина

Елена Репина 2015-04-23 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.
В четырехугольнике $ABCD$ биссектриса угла $C$ пересекает сторону $AD$ в точке $M$ , а биссектриса угла $A$ пересекает сторону $BC$ в точке $K$ . Известно, что $AKCM$ – параллелограмм.
а) Докажите, что $ABCD$ – параллелограмм.
б) Найдите площадь четырехугольника $ABCD$ , если $BK=3$ , $AM=2$ , а угол между диагоналями $AC$ и $BD$ равен $60^{\circ}$ . Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

02 Апр 2015

Задание №18 Т/Р №111 А. Ларина

Елена Репина 2015-04-02 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

На диаметре $AB$ окружности $\omega$ выбрана точка $C$ . На отрезках $AC$ и $BC$ как на диаметрах построены окружности $\omega1$ и $\omega2$ соответственно. Прямая $l$ пересекает окружность $\omega$ в точках $A$ и $D$ , окружность $\omega1$ – в точках $A$ и $E$ , а окружность $\omega2$ – в точках $M$ и $N$ .

а) Докажите, что $MD=NE$ .
б) Найдите радиус круга, касающегося окружностей $\omega$ , $\omega1$ и $\omega2$ , если известно, что $AC=10$ , $BC=6$ .
Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

26 Мар 2015

Задание №18 Т/Р №110 А. Ларина

Елена Репина 2015-03-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.
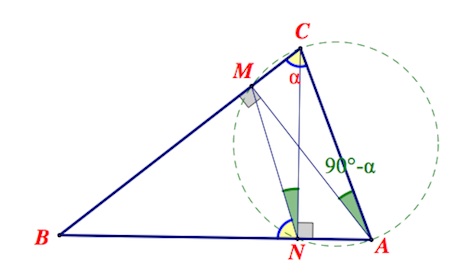
В остроугольном треугольнике $ABC$ проведены высоты $AM$ и $CN$ .
а) Докажите, что углы $ACB$ и $MNB$ равны.
б) Вычислите длину стороны $AC$ , если известно, что периметр треугольника $ABC$ равен $25$ см, периметр треугольника $BMN$ равен $15$ см, а радиус окружности, описанной около треугольника $BMN$ равен $3$ см. Читать далее

Автор: egeMax | комментариев 10

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

19 Мар 2015

Задание №18 Т/Р №109 А. Ларина

Елена Репина 2015-03-19 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.
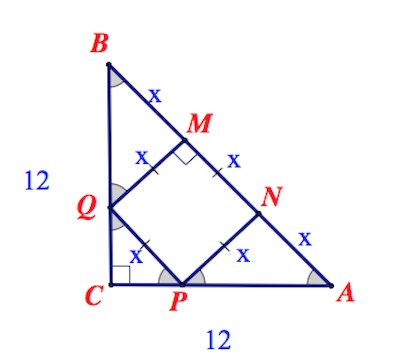
Площадь треугольника $ABC$ равна 72, а сумма длин сторон $AC$ и $BC$ равна 24.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Найдите сторону квадрата, вписанного в треугольник $ABC$ , если известно, что две вершины этого квадрата лежат на стороне $AB$ . Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

12 Мар 2015

Задание №18 Т/Р №108 А. Ларина

Елена Репина 2015-03-12 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

В равнобедренном треугольнике $ABC$ ( $AB=BC$ ) проведены биссектрисы $AK$ , $BM$ , $CP$ .
a) Докажите, что треугольник $KMP$ – равнобедренный.

б) Найдите площадь треугольника $KMP$ , если известно, что площадь треугольника $ABC$ равна 64, а косинус угла $BAC$ равен 0,3.
Читать далее

Автор: egeMax | комментариев 11

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

05 Мар 2015

Задание №18 Т/Р №107 А. Ларина

Елена Репина 2015-03-05 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.
$O$ – точка пересечения диагоналей выпуклого четырехугольника $ABCD$ . Периметры треугольников $AOB$ , $BOC$ , $COD$ и $DOA$ равны между собой.

а) Докажите, что в четырехугольник $ABCD$ можно вписать окружность.
б) Найдите радиус окружности, вписанной в треугольник $DOA$ , если радиусы окружностей, вписанных в треугольники $AOB$ , $BOC$ и $COD$ равны соответственно 3, 4 и 6. Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

26 Фев 2015

Задание №18 Т/Р №106 А. Ларина

Елена Репина 2015-02-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

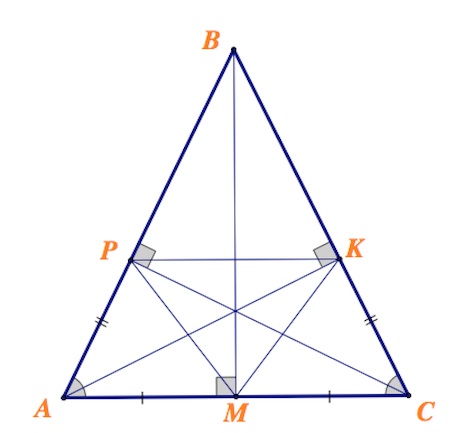
В равнобедренном треугольнике $ABC$ ( $AB=BC$ ) проведены высоты $AK$ , $BM$ и $CP$ .

a) Докажите, что треугольник $KMP$ – равнобедренный.

б) Найдите площадь треугольника $ABC$ , если известно, что площадь треугольника $KMP$ равна 12, а косинус угла $ABC$ равен 0,6.

Автор: egeMax | комментария 3

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

19 Фев 2015

Задание №18 Т/Р №105 А. Ларина

Елена Репина 2015-02-19 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

Окружность касается стороны $AB$ параллелограмма $ABCD$ , пересекает стороны $AD$ и $BC$ в точках $M$ и $N$ соответственно и проходит через вершины $C$ и $D$ .
а) Докажите, что $DN=CM$ .
б) Найдите $DN$ , зная, что $AM=9$ , $BN=16$ , $ВС=18.$
Читать далее

Автор: egeMax | Нет комментариев

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

1 2 3 4 Вперед »