Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Рассмотрим следующее задание С3 из Т/Р №60 А. Ларина.
Архив по категории: Модуль
22
Янв 2014
С3 (№17) с логарифмами и модулями
Елена Репина 2014-01-22 2023-07-24Автор: |
комментария 4
04
Окт 2013
Задача 23 из второй части ГИА по математике
Елена Репина 2013-10-04 2023-08-03Произведем разбор задачи 23 из модуля “Алгебра”, которая предлагалась на Тренировочной работе № 1 в формате ГИА 1 октября 2013 года.
Постройте график функции y =|x −1| − |x +1| + x и найдите все значения k , при которых прямая y = kx имеет с графиком данной функции ровно одну общую точку. Читать далее
Автор: |
комментария 3
13
Июл 2013
Разбор задания из пробного экзамена в МГУ в 2013 году. Система неравенств.
Елена Репина 2013-07-13 2023-08-07
21
Июн 2013
Неравенство с двумя модулями. Часть II
Елена Репина 2013-06-21 2023-08-08«Неравенство с двумя модулями. Часть I» смотрим здесь.
Решим неравенство $ |4-x|+|x^2+x-6|\geq 7$
Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них. Читать далее
21
Июн 2013
Неравенство, содержащее в себе несколько модулей. Часть I
Елена Репина 2013-06-21 2023-08-08В видеоролике рассматривается решение следующего неравенства с модулями:
$|x| – 2|x+1| + 3|x+2| \geq 4$
Показаны два способа оформления.
Похожее задание для самостоятельной проработки:
$2|x-3| + |x+1| \leq 3x+1$ (Ответ: $[1,5;+\infty)$)
«Неравенство, содержащее в себе несколько модулей. Часть II» смотрим здесь.
19
Июн 2013
Тест «Простейшие неравенства с модулем»
Елена Репина 2013-06-19 2015-08-21Автор: |
комментариев 18
18
Июн 2013
Тест по теме «Модуль. Простейшие уравнения с модулем»
Елена Репина 2013-06-18 2015-08-21
18
Июн 2013
Модуль. Раскрытие модуля. Простешие уравнения с модулем
Елена Репина 2013-06-18 2023-08-08Определение. Геометрический смысл
Модуль (или абсолютная величина)числа $x$ (обозначается как $|x|$)— неотрицательное число, определение которого зависит от типа числа $x.$
А именно:
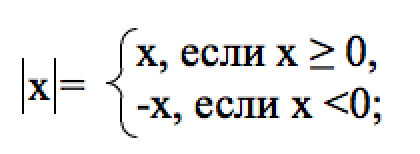
Мы будем называть данное правило правилом раскрытия модуля.
Автор: |
комментария 4
11
Июн 2013
Модуль. Простейшие неравенства с модулем.
Елена Репина 2013-06-11 2023-08-08Определение модуля, правило раскрытия смотрим здесь
Неравенства с модулем вида
$\color{red}|f(x)|\leq g(x)$ (или$\color{red}|f(x)|<g(x)$)
[spoiler]
Неравенства указанного вида можно решать, исходя из определения модуля, опираясь на правило раскрытия модуля. Но зачастую целесообразно переходить к системе неравенств: Читать далее
