Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Основные способы разложения многочлена на множители
1. Вынесение общего множителя за скобку
$\quad{\bigtriangleup \cdot \bigcirc +\bigtriangleup \cdot \bigstar =\bigtriangleup (\bigcirc +\bigstar )}$
Архив по категории: Справочные материалы
22
Фев 2013
Разложение на множители
Елена Репина 2013-02-22 2023-07-06
20
Фев 2013
Тригонометрические формулы
Елена Репина 2013-02-20 2023-08-11Основные тригонометрические формулы
$\sin^2\alpha + cos^2 \alpha= 1$ Видео*
$tg\alpha =\frac{\sin\alpha }{\cos \alpha},\;ctg\alpha =\frac{\cos\alpha}{\sin\alpha}$
$tg^2\alpha + 1 = \frac{1}{\cos^2\alpha},\;ctg^2 \alpha + 1 = \frac{1}{\sin^2\alpha}$
20
Фев 2013
Степень числа. Корень
Елена Репина 2013-02-20 2023-08-11Натуральная степень числа
Число c называется n-й степенью числа a ( обозначается как $\color{ red} a^{n}$), если
$\color{red} c=\underbrace {a\cdot a\cdot…\cdot a}_{n\;{times}}$
18
Фев 2013
Логарифм. Определение. Свойства логарифмов
Елена Репина 2013-02-18 2023-07-06Логарифм числа $b$ по основанию $a$ определяется как показатель степени, в которую нужно возвести основание $a$, чтобы получить число $b$.
Обозначение $log_a b$ читается как логарифм $b$ по основанию $a$.
Например, $log_28=3$, так как $2^3=8$ ($2$ – основание степени, $3$ – показатель степени)
ЛОГАРИФМЫ
$\Large{\log_{a}b=c\Leftrightarrow a^{c}=b\;}\;$
17
Фев 2013
Производная функции. Геометрический смысл
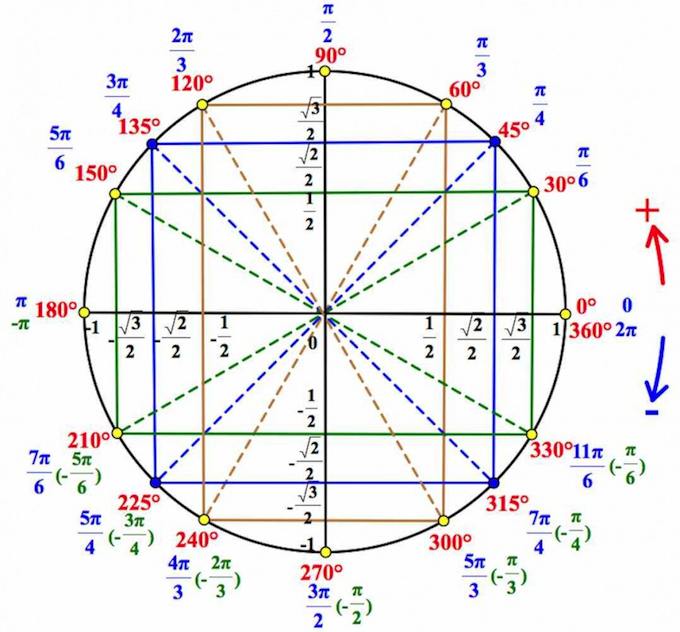
Елена Репина 2013-02-17 2021-06-30
17
Фев 2013
Тригонометрический круг. Основные значения тригонометрических функций
Елена Репина 2013-02-17 2021-06-18
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг: Читать далее
17
Фев 2013
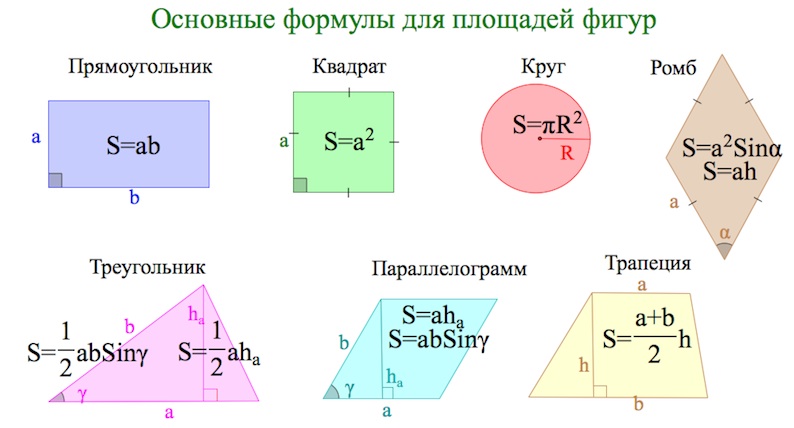
Площади фигур
Елена Репина 2013-02-17 2014-02-10Площади основных фигур. Набор формул
Эта таблица хороша для начального знакомства с темой “Площади фигур”.
Для более подготовленных учеников интересна будет расширенная таблица (!)
