Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Смотрите также № 17, №18
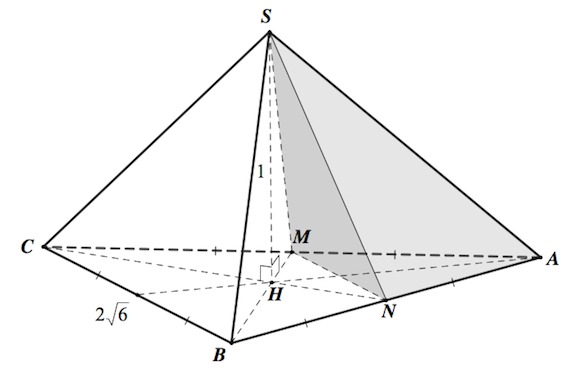
Сторона основания правильной четырехугольной пирамиды равна $\sqrt6$, боковое ребро составляет с высотой угол $30^{\circ}$. Плоскость $\alpha$, проходящая через вершину основания пирамиды, перпендикулярна противолежащему боковому ребру и разбивает пирамиду на две части. Читать далее
Архив по категории: Т/P A. Ларина
24
Сен 2014
№16 (С2 по старому) из Тренировочного варианта №84 А. Ларина
Елена Репина 2014-09-24 2023-07-22Автор: |
комментария 4
24
Сен 2014
№17 Тренировочной работы №84 А. Ларина
Елена Репина 2014-09-24 2023-07-22Смотрите также задания №16, №18 Читать далее
Автор: |
комментария 2
24
Сен 2014
№ 18 (C4) Тренировочной работы №84 А. Ларина
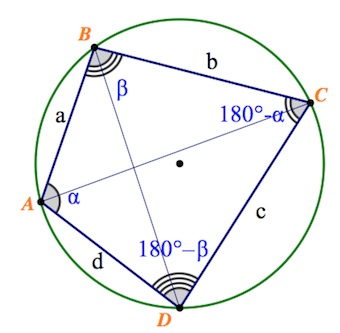
Елена Репина 2014-09-24 2023-07-22Вокруг выпуклого четырёхугольника со сторонами $a,$ $b,$ $c,$ $d$ описана окружность.
а) Докажите, что отношение длин его диагоналей выражается как $\frac{bc+ad}{ab+cd}$;
б) Найдите площадь четырёхугольника, если $a=2$, $b=8$, $c=12$, $d=4$. Читать далее
Автор: |
Нет комментариев
05
Мар 2014
C3 Т/Р №66 Ларина
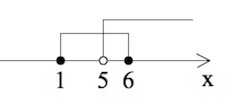
Елена Репина 2014-03-05 2023-07-23Решите систему неравенств:
$\begin{cases}log_2(5-x)(2-x)>log_4(x-2)^2,\\\frac{2^x-2^{2-x}-3}{2^x-2}\geq 0;&\end{cases}$
Автор: |
Нет комментариев
19
Фев 2014
С2 (№16)
Елена Репина 2014-02-19 2023-07-23Автор: |
комментариев 6
12
Фев 2014
С4 (№18) нового образца
Елена Репина 2014-02-12 2023-07-23Автор: |
комментария 2
12
Фев 2014
C5 (№20) с ловушкой, не попадитесь!
Елена Репина 2014-02-12 2023-07-23Автор: |
комментария 4
11
Фев 2014
С1 (№15). Иррациональное уравнение с тригонометрическими функциями
Елена Репина 2014-02-11 2023-07-23Автор: |
комментариев 5
11
Фев 2014
С2 (№16) на нахождение радиуса вписанной в тетраэдр сферы
Елена Репина 2014-02-11 2023-07-23Автор: |
комментариев 8
22
Янв 2014
С3 (№17) с логарифмами и модулями
Елена Репина 2014-01-22 2023-07-24
Рассмотрим следующее задание С3 из Т/Р №60 А. Ларина.
Автор: |
комментария 4
22
Янв 2014
C4, пересекающиеся окружности с общей касательной
Елена Репина 2014-01-22 2023-07-24
С4 Тренировочной работы №60 А. Ларина
Автор: |
Нет комментариев
22
Янв 2014
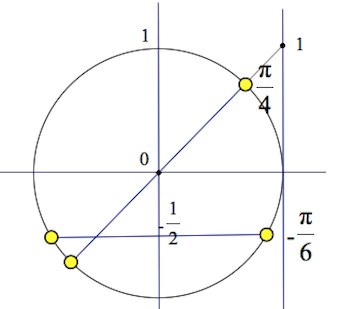
С1 (№15) с отбором корней на отрезке
Елена Репина 2014-01-22 2023-07-24Вы можете также посмотреть задание С3(№17), задание С4(№18) Т/Р. Читать далее
Автор: |
комментария 22
14
Янв 2014
Ну очень красивое задание С2 (№16) ЕГЭ по математике!
Елена Репина 2014-01-14 2023-07-24Автор: |
комментариев 6
26
Дек 2013
Видеорешение задачи С4 (№18) ЕГЭ по математике
Елена Репина 2013-12-26 2023-07-24
Видеорешение задачи С4 Тренировочной работы №56 А. Ларина
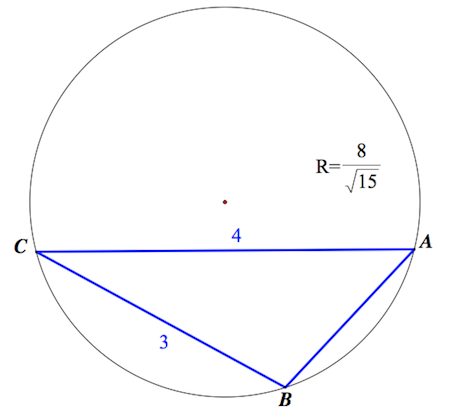
В окружность вписан четырехугольник $ABCD$, диагонали которого взаимно перпендикулярны и пересекаются
в точке $E$. Прямая, проходящая через точку $E$ и перпендикулярная к $AB$, пересекает сторону $CD$ в точке $M$.
а) Докажите, что $EM$ – медиана треугольника $CED$
б) Найдите $EM$, если $AD = 8$ , $AB = 4$ и угол $CDB$ равен 60°.
Автор: |
Нет комментариев
25
Дек 2013
С2 (№16) Тренировочной работы №56 А. Ларина
Елена Репина 2013-12-25 2023-07-24
Приглашаю посмотреть видеорешение задачи категории С2 на нахождение угла между плоскостями.
В основании прямой призмы ABCDA’B’C’D’ лежит ромб ABCD со стороной $\sqrt{21}$ и углом А, равным 60°. На ребрах AB , B’C’ и DC взяты соответственно точки E, F и G так, что AE=EB, B’F=FC’ и DG=3GC. Найдите косинус угла между плоскостями EFG и ABC, если высота призмы равна 4,5.
Автор: |
комментария 4
