Ранее задание значилось под №15. Сейчас – под №13 (С1).
Смотрите также №16, №17, №18, №19, №20.
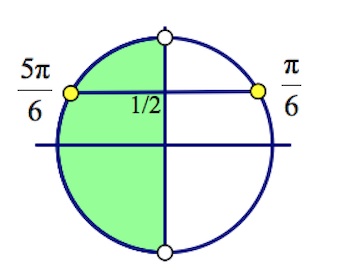
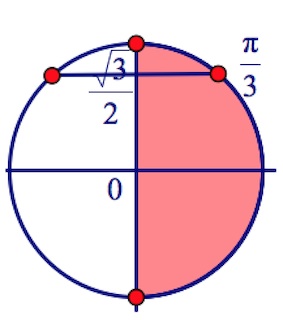
Дано уравнение $(0,25)^{cos(\frac{3\pi}{2}+x)}=2^{cos2x-1}.$
а) Решите уравнение;
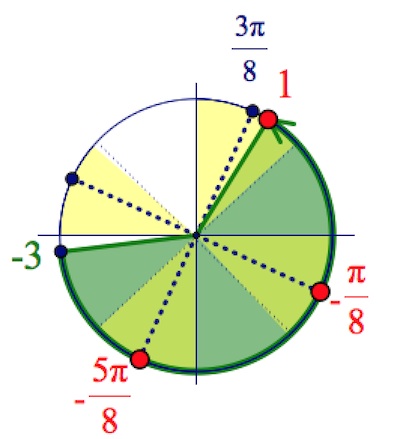
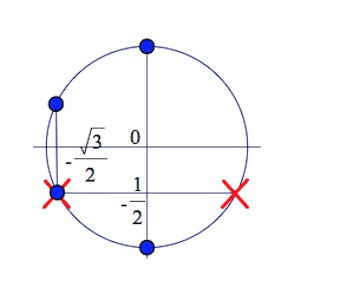
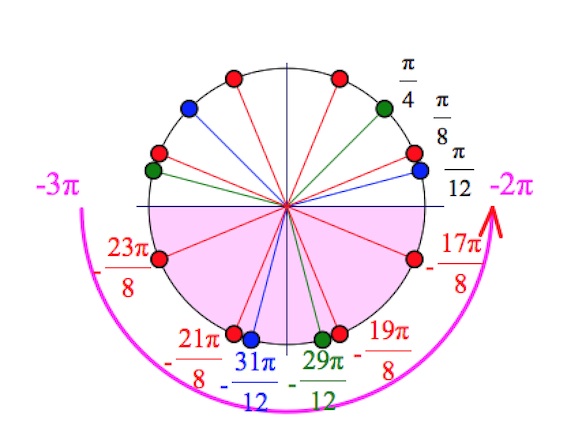
б) Укажите корни этого уравнения, принадлежащие отрезку $[-\frac{15\pi}{4};-3\pi].$ Читать далее