Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Видеоразбор С5
Продолжаем готовиться к ЕГЭ по математике. Учимся решать задания части С.
При каких действительных значениях параметра a система
$\begin{cases}
3|x|+2|y|=12,\\x^2 +y^2=a^2;
\end{cases}$
имеет наибольшее число решений? Читать далее
Архив по категории: Видеоуроки
23
Май 2013
Егэ, С5 (№20). Система с параметром
Елена Репина 2013-05-23 2023-08-10
07
Май 2013
ЕГЭ, С2 (№16). Угол между плоскостями в призме
Елена Репина 2013-05-07 2023-08-10Задача С2 (в новом формате ЕГЭ по математике – «Задание №14»)
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ стороны основания равны $1$ , а боковые ребра равны $5$. На ребре $AA_1$ отмечена точка $E$ так, что $AE:EA_1=2:3$. Найдите угол между плоскостями $ABC$ и $BED_1$. Читать далее
03
Май 2013
с2 (№16), досрочный егэ 2013
Елена Репина 2013-05-03 2015-09-04Видеоразбор части С
Здесь смотрим разбор С4(№18), С5(№20) из досрочного ЕГЭ по математике за 2013 г.
А сейчас разбираем стереометрическую задачу С2 (в новом формате ЕГЭ по математике – «Задание №14») из досрочного ЕГЭ. Читать далее
30
Апр 2013
ГИА, часть 2, геометрическая задача на свойство биссектрисы
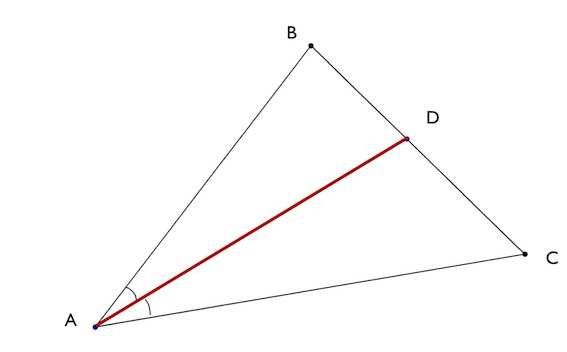
Елена Репина 2013-04-30 2023-08-10В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 17:15, считая от точки В. Найдите радиус окружности, описанной около треугольника АВС, если ВС=24
29
Апр 2013
ЕГЭ, С5 (№20). Уравнение c параметром
Елена Репина 2013-04-29 2023-08-11
Найдите все значения параметра а, при которых уравнение $a|x-4| = \frac{5}{x+1}$ на промежутке $[0; +\infty)$ имеет ровно три корня. Читать далее
28
Апр 2013
Геометрическая задача части II ГИА
Елена Репина 2013-04-28 2023-08-11Медианы △АВC пересекаются в точке М. Найдите длину медианы, проведенной к стороне ВC, если ∠ВАC=47°, ∠ВМC=133°, ВC=4√3
20
Апр 2013
ГИА, задача II части
Елена Репина 2013-04-20 2023-08-11Длины двух сторон треугольника равны 4 и 5, а угол между ними равен 30°. В этот угол вписали окружность, центр которой находится на третьей стороне треугольника. Найдите радиус этой окружности
08
Апр 2013
ЕГЭ, С4. Задача об окружности, касающейся двух других (и их общей касательной)
Елена Репина 2013-04-08 2023-08-11
Продолжаем готовится к ЕГЭ по математике. Учимся решать задачи части С.
Две окружности, радиусы которых 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной. Читать далее
08
Апр 2013
ЕГЭ, С4 (№18). Вневписанные окружности
Елена Репина 2013-04-08 2023-08-11
Продолжаем готовится к ЕГЭ по математике. Учимся решать задачи категории С4.
Две окружности, радиусы которых 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной Читать далее
15
Мар 2013
Элементы треугольника. Биссектриса
Елена Репина 2013-03-15 2023-08-11Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
