Подготовка к ЕГЭ по математике

(ЕГЭ 2023, Досрок)

Найдите все значения a, при каждом из которых множество решений неравенства

$\large \frac{5-a-(a^2-2a+1)sinx}{cos^2x+a^2+2}<1$

содержит отрезок $[0;\frac{2\pi}{3}].$

Решение:

Так как $cos^2x+a^2+2>0$ всегда, то переходим к равносильному неравенству:

$5-a-(a^2-2a+1)sinx-cos^2x-a^2-2<0;$

$5-a-(a^2-2a+1)sinx-(1-sin^2x)-a^2-2<0;$

$sin^2x-(a-1)^2sinx-a^2-a+2<0.$

Пусть $sinx=m,m\in[-1;1].$

Заметим, если $x\in[0;\frac{2\pi}{3}],$ то $m\in[0;1].$

Пусть $f(m)=m^2-(a-1)^2m-a^2-a+2.$

Хотим, чтобы решения неравенства $f(m)<0$ содержали бы в себе отрезок $[0;1].$

Достаточно потребовать:

$\begin{cases}f(0)<0,&&f(1)<0;&\end{cases}$

$\begin{cases}-a^2-a+2<0,&&1-(a-1)^2-a^2-a+2<0;&\end{cases}$

$\begin{cases}a^2+a-2>0,&&2a^2-a-2>0;&\end{cases}$

Ответ: $(-\infty;-2)\cup (\frac{1+\sqrt{17}}{4};+\infty).$

(ЕГЭ 2023, Досрок)
Найдите все значения параметра a, при каждом из которых уравнение [latexpage]

$\sqrt{5x-3}\cdot ln(x^2-6x+10-a^2)=0$

имеет ровно один корень на отрезке $[0;3].$

Решение:

$\sqrt{5x-3}\cdot ln(x^2-6x+10-a^2)=0;$

$\begin{cases}\sqrt{5x-3}=0,\\x^2-6x+10-a^2>0;&\end{cases}\quad $ или $\quad \begin{cases}ln(x^2-6x+10-a^2)=0;\\5x-3\geq 0;&\end{cases}$

$\begin{cases}x=0,6,\\(\frac{3}{5})^2-6\cdot \frac{3}{5}+10-a^2>0;&\end{cases}\quad $ или $\quad \begin{cases}x^2-6x+10-a^2=1;\\x\geq 0,6;&\end{cases}$

$\begin{cases}x=0,6,\\(a-2,6)(a+2,6)<0;&\end{cases}\quad $ или $\quad \begin{cases}a=\pm (x-3);\\x\geq 0,6;&\end{cases}$

Работаем в системе координат $(x;a).$ При этом рабочая зона – $x\in [0;3].$

Множество точек, отвечающее исходному уравнению, помечено на рисунке красным цветом (жирные линии).
Откуда видно, что уравнение имеет единственное решение при $a \in (-2,6;-2,4]\cup [2,4;2,6).$

Ответ: $(-2,6;-2,4]\cup [2,4;2,6).$

(ЕГЭ 2023, Досрок)

Найдите все значения параметра a, при каждом из которых уравнение [latexpage]

$\sqrt{3x-5}\cdot ln(4x^2-a^2)=\sqrt{3x-5}\cdot ln(2x+a)$

имеет ровно один корень.

Решение:

$\sqrt{3x-5}\cdot ln(4x^2-a^2)=\sqrt{3x-5}\cdot ln(2x+a);$

$\sqrt{3x-5}\cdot(ln(4x^2-a^2)- ln(2x+a))=0;\\$

$\\$

$\Bigg[\begin{array}{rl}\sqrt{3x-5}=0,\\ln(4x^2-a^2)- ln(2x+a)=0;\end{array}\quad $ при условии $\quad \begin{cases}3x-5\geq 0,\\2x+a>0,\\4x^2-a^2>0;\end{cases}\\$

$\\$

$\\ \Bigg[\begin{array}{rl}3x-5=0,\\(2x+a)(2x-a-1)=0;\end{array}\quad $ при условии $\quad \begin{cases}3x-5\geq 0,\\2x+a>0,\\(2x-a)(2x+a)>0;\end{cases}$

$\Bigg[\begin{array}{rl}\\x=\frac{5}{3},\\a=-2x,\\a=2x-1;\\\\ \end{array}\quad $ при условии$\quad \begin{cases}x\geq \frac{5}{3},\\a>-2x,\\(2x-a)(2x+a)>0;\end{cases}$

Работаем в системе координат (x;a).

Множество точек, отвечающее исходному уравнению, помечено на рисунке красным цветом.
Откуда видно, что уравнение имеет единственное решение при $a \in(-\frac{10}{3};\frac{7}{3}]\cup [\frac{10}{3};+\infty).$

Ответ: $(-\frac{10}{3};\frac{7}{3}]\cup [\frac{10}{3};+\infty).$

(ЕГЭ 2023, Досрок)

Окружность касается одной из сторон прямого угла с вершиной $D$ в точке $E$ и пересекает вторую сторону в точках $A$ и $B$ (точка $A$ лежит между $B$ и $D$). В окружности проведён диаметр $AC.$

а)  Докажите, что отрезок $BC$ вдвое больше отрезка $DE$.

б)  Найдите расстояние от точки $E$ до прямой $AC,$ если $AD = 4$ и $AB = 5.$

Решение:

а) $\angle ABC=90^{\circ},$ так как опирается на диаметр $AC.$

 Пусть $K$ – середина $AB.$ В равнобедренном треугольнике $AOB$ ($AO=OB$ как радиусы) медиана $OK$  – высота.

$OE\perp DE$ как радиус, проведенный к касательной.

Таким образом $DEOK$ – прямоугольник и $OK=DE.$

При этом $OK$ – средняя линия треугольника $ABC,$ то есть $OK=\frac{BC}{2}.$

Итак, $BC=2OK=2DE.$

б) Пусть $EH$ – искомое расстояние. Пусть  $OE=AO=R.$

Из треугольника $AOK:$

$OK=\sqrt{AO^2-AK^2}=\sqrt{R^2-2,5^2}.$

$DE=OK=\sqrt{R^2-(\frac{5}{2})^2}$ – расстояние от точки $A$ до $EO.$

По свойству касательной и секущей:

$DE^2=DA\cdot DB;$

$R^2-2,5^2=4\cdot 9;$

$R=6,5.$

Заметим, треугольник $AEO$ – равнобедренный, значит высоты, проведенные к боковым сторонам, равны.

Длина $EH$ равна расстоянию от $A$ до $EO:$

$\rho (E,AC)=DE=\sqrt{R^2-2,5^2}=\sqrt{6,5^2-2,5^2}=6.$

Ответ: $6.$

(ЕГЭ 2023, Досрок)

Серединный перпендикуляр к стороне $AB$ треугольника $ABC$ переcекает сторону $AC$ в точке $D.$ Окружность с центром $O,$ вписанная в треугольник $ADB,$ касается отрезка $AD$ в точке $P,$ а прямая $OP$ пересекает сторону $AB$ в точке $K.$

а)  Докажите, что около четырёхугольника $BDOK$ можно описать окружность.

б)  Найдите радиус окружности, описанной около четырёхугольника $BDOK,$ если $AB=10,BC=\sqrt{19},AC=9.$

Решение:

а) Серединный перпендикуляр к $AB$ – биссектриса угла  $ADB.$

Пусть $\angle DAB=\angle DBA=\alpha.$ Тогда $\angle ADH= \angle BDH=90^{\circ}-\alpha,$ где $H$ – середина $AB.$

Тогда, с учетом того, что  $OP\perp AC,$ получаем: $\angle POD=\alpha.$ И тогда $\angle DOK=180^{\circ}-\alpha.$

Итак, в четырехугольнике $BDOK$ наблюдаем:

$\angle O+\angle B=180^{\circ}-\alpha+\alpha=180^{\circ},$

что говорит о том, около четырёхугольника можно описать окружность.

б) Заметим, треугольник $ABC$ – прямоугольный, так как $10^2=9^2+(\sqrt{19})^2$.

Пусть $DC=x,$ тогда $AD=DB=9-x.$

Из треугольника $DBC:$

$(9-x)^2=x^2+19;$

$62=18x;$

$x=\frac{31}{9}.$

Тогда  $DB=9-x=9-\frac{31}{9}=\frac{50}{9}.$

Замечаем, $BO$ – биссектриса угла $DBA.$

Из треугольника $DOB:$

$\angle DOB=180^{\circ}-\alpha-(90^{\circ}-\frac{\alpha}{2})=90^{\circ}-\frac{\alpha}{2}.$

Из треугольника $ABC$ $cosA=cos \alpha=\frac{9}{10}.$

Тогда $cos\frac{\alpha}{2}=\sqrt{\frac{cos\alpha+1}{2}}=\sqrt{\frac{19}{20}}.$
 По теореме Синусов для треугольника $DBO:$

$\frac{DB}{sinDOB}=2R;$

$\frac{\frac{50}{9}}{sin(90^{\circ}-\frac{\alpha}{2})}=2R;$

$\frac{\frac{50}{9}}{cos\frac{\alpha}{2}}=2R;$

$R=\frac{25}{9cos\frac{\alpha}{2}};$

$R=\frac{25}{9\cdot \sqrt{\frac{19}{20}}};$

$R=\frac{25\sqrt{20}}{9\sqrt{19}};$

$R=\frac{50\sqrt{95}}{171}.$

Ответ: $\frac{50\sqrt{95}}{171}.$

(ЕГЭ 2023, Досрок)

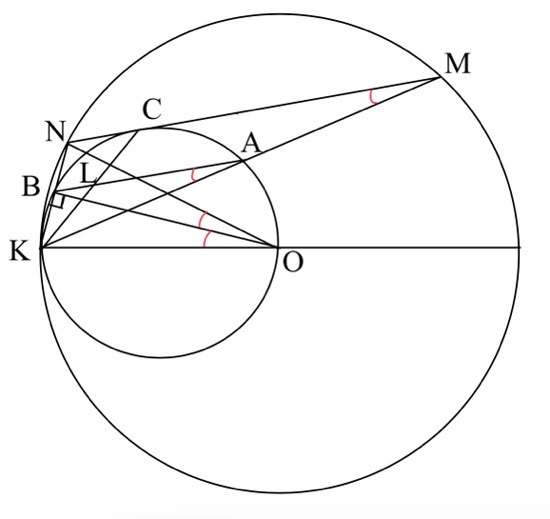
Две окружности касаются внутренним образом в точке $K,$ причём меньшая проходит через центр большей. Хорда $MN$ большей окружности касается меньшей в точке $C.$ Хорды $KM$ и $KN$ пересекают меньшую окружность в точках $A$ и $B$ соответственно, а отрезки $KC$ и $AB$ пересекаются в точке $L.$

а)  Докажите, что $CN:CM=LB:LA.$

б)  Найдите длину хорды $MN,$ если $LB:LA=3:7,$  a радиус меньшей окружности равен $\sqrt{17}.$

Решение:

а) Пусть $O$ – центр большей окружности.

Угол $KBO$ – прямой, так как опирается на диаметр   $KO.$

$OB$ – радиус, проведенный перпендикулярно хорде $KN,$ а значит $B$ – середина $KN.$ Тогда $BO$ – не только высота и медиана в треугольнике $KON,$ но и биссектриса.

Пусть

$\angle BOK=\angle NOB=\alpha.$

При этом

$\angle BAK=\angle BOK=\alpha$ (опираются на одну дугу).

Далее,

$\angle NMK=\frac{1}{2}\angle NOK$ (пара “центральный-вписанный”)

$\angle NMK=\frac{2\alpha}{2}=\alpha.$

Имеем: $\angle BAK=\angle NMK=\alpha,$ значит прямые $NM, AB$ параллельны.

Но тогда $\triangle KBL\infty \triangle KNC$ и $\triangle KLA\infty \triangle KCM.$

А значит, $LB:CN=KL:KC$ и $LA:CM=LK:CK,$ откуда

$LB:CN=LA:CM$

или

$CN:CM=LB:LA.$

б) Пусть $Q$ – центр малой окружности. $QC\perp NM.$

Пусть $OT\perp NM$ ($T$ – середина  $NM$).

По условию $LB:LA=3:7,$ значит $NC:CM=3:7.$ Пусть $NC=3x,CM=7x,$ тогда $CT=2x.$

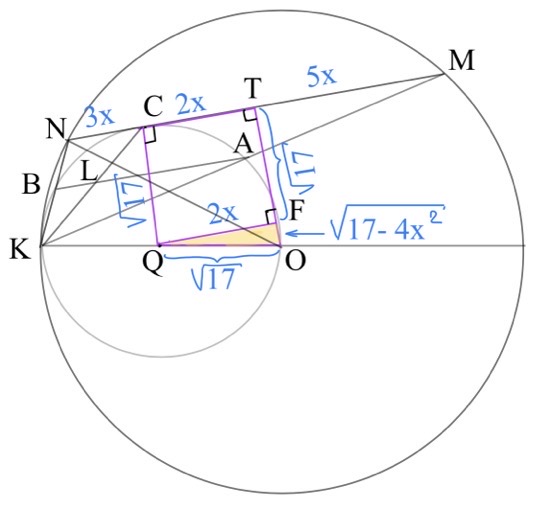
Пусть $QF\perp OT.$

Очевидно, $QC=FT=\sqrt{17},CT=QF=2x.$

Из треугольника $QOF:$

 $FO=\sqrt{17-4x^2}.$

Наконец, из треугольника  $NTO$ имеем:

$NO^2=NT^2+TO^2;$

$4\cdot 17=(5x)^2+(\sqrt{17}+\sqrt{17-4x^2})^2;$

$4\cdot 17=25x^2+17+2\sqrt{17(17-4x^2)}+17-4x^2;$

$2\sqrt{17(17-4x^2)}=34-21x^2;$

$4(17^2-68x^2)=(34-21x^2)^2;$

$4(17^2-68x^2)=34^2-68\cdot 21x^2+441x^4;$

$441x^4=17\cdot 68x^2;$

$21x^2=34^2;$

$x=\frac{34}{21}.$

Тогда

$MN=10x=\frac{340}{21}.$

Ответ: $\frac{340}{21}.$

Полезно посмотреть аналог

ЕГЭ 2023, Досрок
Точка $B$ лежит на отрезке $AC$. Прямая, проходящая через точку $A$, касается окружности с диаметром $BC$ в точке $M$ и второй раз пересекает окружность с диаметром $AB$ в точке $K.$ Продолжение отрезка $MB$ пересекает окружность с диаметром $AB$ в точке $D.$

а)  Докажите, что прямые $AD$ и $MC$ параллельны.

б)  Найдите площадь треугольника $DBC$, если $AK=7$ и $MK=14.$

Решение:

а) Заметим, углы $BMC, ADB$ опираются на диаметр, а значит являются прямыми. Стало быть, углы при прямых $AD,$ $MC$ и секущей $DM$ равны. А значит, по признаку параллельности прямых, $AD$ и $MC$ параллельны.

б) Пусть $Q$ – середина $BC.$ Заметим, $MQ$ перпендикулярен $AM$ как радиус, проведенный к касательной.

Треугольники $AKB$, $AMQ$ подобны по двум углам (угол A общий и углы $AKM, AMQ$ прямые).

С учетом условия $AK=7$ и   $MK=14$ коэффициент подобия треугольников – $1:3.$

Пусть $AB=2x,BQ=MQ=4x,$ $BK=\frac{4}{3}MQ=\frac{4}{3}x.$

Из треугольника $AKB$ по теореме Пифагора:

$4x^2=49+(\frac{4x}{3})^2;$

$36x^2=49\cdot 9+16x^2;$

$20x^2=49\cdot 9;$ с.

$x=\frac{21}{2\sqrt{5}}.$

$BK=\frac{4}{3}x=\frac{14}{\sqrt{5}}.$

Заметим, треугольники $ABM,$ $CBD$ равновелики.
Действительно, с учетом параллельности прямых $AD$ и $MC,$ имеем:

$S_{CBD}=S_{ACD}-S_{ABD}=S_{AMD}-S_{ABD}=S_{AMB}.$

Итак,

$S_{CBD}=S_{AMB}=\frac{AM\cdot BK}{2}=\frac{21\cdot \frac{14}{\sqrt{5}}}{2}=\frac{147\sqrt 5}{5}.$

Ответ: $\frac{147\sqrt5}{5}.$

3.1. (ЕГЭ 2023, Досрок)

15 января Алексей планирует взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата следующие:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r  — целое число;

— платёж должен вноситься один раз в месяц, со 2-го по 14-е число каждого месяца;

— 15-го числа каждого месяца размер долга должен соответствовать долгу, указанному в таблице.

Решение:

Пусть $k=\frac{r}{100}.$

Распишем платежи каждого месяца:

1. $0,2+k\cdot 1$
2. $0,1+k\cdot 0,8$
3. $0,2+k\cdot 0,7$
4. $0,2+k\cdot 0,5$
5. $0,2+k\cdot 0,3$
6. $0,1+k\cdot 0,1$

Общая сумма выплат: $1+k(1+0,8+0,7+0,5+0,3+0,1).$

По условию общая сумма платежей больше $1,4$ млн рублей, поэтому

$1+k(1+0,8+0,7+0,5+0,3+0,1)>1,4;$

$1+3,4k>1,4;$

$k>\frac{1,4-1}{3,4};$

$k>\frac{2}{17}.$

Откуда

$\frac{r}{100}>\frac{2}{17};$

$r>\frac{200}{17};$

$r>11\frac{13}{17}.$

Наименьшее целое число $r,$ отвечающее неравенству, – это $12.$

 Ответ: $12.$

(ЕГЭ 2023, Досрок)

В июле 2023 года планируется взять кредит на некоторую сумму. Условия возврата таковы:

— в январе каждого года долг увеличивается на $20$% по сравнению с предыдущим годом;

— с февраля по июнь нужно выплатить часть долга одним платежом.

Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года), а общая сумма выплат равна $311 040$ рублей?

Решение:

Пусть $S$ – сумма кредита. Пусть $x$- сумма каждой из четырех выплат.

Распишем остатки долга после каждого погашения:

2024 год: $1,2S-x;$

2025 год: $1,2^2S-1,2x-x;$

2026 год: $1,2^3S-1,2^2x-1,2x-x;$

2027 год: $1,2^4S-1,2^3x-1,2^2x-1,2x-x=0$ (*)

Ссогласно условию $4x=311040$, значит $x=77760.$

Тогда, возвращаясь к (*), имеем:

$1,2^4\cdot S-77760\cdot (1,2^3+1,2^2+1,2+1)=0;$

$S=\frac{77760\cdot (1,2^3+1,2^2+1,2+1)}{1,2^4};$

$S=\frac{77760\cdot ((\frac{6}{5})^3+(\frac{6}{5})^2+\frac{6}{5}+1)}{(\frac{6}{5})^4};$

$S=\frac{5\cdot 77760\cdot (6^3+5\cdot 6^2+25\cdot 6+125)}{6^4};$

$S=201300.$

Ответ: $201300$ рублей.

(ЕГЭ 2023, Досрок)
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: 

—  каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; 

—  с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на $104 800$ рублей больше суммы, взятой в кредит?

Решение:

Пусть $S$ – сумма кредита. Пусть $x$- сумма каждой из трех выплат (в тыс. руб.).

Распишем остатки долга после каждого погашения:

2021 год: [latexpage]$1,25S-x;$

2022 год: $1,25^2S-1,25x-x;$

2023 год: $1,25^3S-1,25^2x-1,25x-x=0$ (*)

Общая сумма выплат $3x$ на $104800$ рублей больше суммы $S$, взятой в кредит, согласно условию, поэтому

Общая сумма выплат $3x$ на $104800$ рублей больше суммы $S$, взятой в кредит, согласно условию, поэтому

$S=3x-104800.$

Тогда, возвращаясь к (*), имеем:

$1,25^3\cdot (3x-104800)-x(1,25^2+1,25+1)=0;$

$x(1,25^3\cdot 3-1,25^2-1,25-1)-1,25^3\cdot 104800=0;$

$x=\frac{1,25^3\cdot 104800}{1,25^3\cdot 3-1,25^2-1,25-1};$

$x=\frac{(\frac{5}{4})^3\cdot 104800}{(\frac{5}{4})^3\cdot 3-(\frac{5}{4})^2-\frac{5}{4}-1};$

$x=\frac{5^3\cdot 104800}{3\cdot 5^3-4\cdot 5^2-16\cdot 5-64};$

$x=300.$

Ответ: $300000.$

(Досрок 2023)

Решите неравенство: $\large \frac{4^x-2^{x-3}+7}{4^x-5\cdot 2^x+4}\leq \frac{2^x-9}{2^x-4}+\frac{1}{2^{x}-6}.$

Решение:

Ответ: $(-\infty;0)\cup(0;2)\cup (log_26;3].$

(Досрок 2023)

Решите неравенство: $\Large \frac{8^{x+\frac{2}{3}}-9\cdot 4^{x+\frac{1}{2}}+13\cdot2^x-13}{4^{x+\frac{1}{2}}-9\cdot 2^{x}+4}\leq \large 2^{x+1}-\Large\frac{1}{2^x-2}+\frac{3}{2^{x+1}-1}.$

Решение:

Ответ: $(-\infty;-1)\cup(-1;1)\cup [log_23;2).$

(Досрок 2023)

Решите неравенство: $\large \frac{9^x-3^{x+1}-19}{3^x-6}+\frac{9^{x+1}-3^{x+4}+2}{3^x-9}\leq 10\cdot 3^x+3.$

Решение:

$(-\infty;1]\cup(log_36;2).$

(Пробный ЕГЭ-23)

Решите неравенство: $\large \log_{4}( x-3) (10+3x-x^{2}) +\log_{4}\frac{7-x}{10+3x-x^{2}}\leq -1+\log _{4}( 2x+4).$

Решение:

Ответ: $ ( 3; 4].$

(Досрок 2023) 

а)  Докажите, что плоскость KML содержит точку B.

В основании пирамиды SABCD лежит параллелограмм ABCD. На боковых рёбрах SA, SC и SD отмечены точки K, L и M соответственно так, что SK : KA  =  SL : LC  =  2 : 1 и SM  =  MD.

б)  Найдите объём пирамиды BAKMD, если площадь параллелограмма ABCD равна 18, а высота пирамиды SABCD равна 7.

Решение:

Ответ: 14.