Главная › 14 (С3) Неравенства › Диагностическая работа (декабрь 2013). Задание С3

13 Дек 2013

Категория: 14 (С3) НеравенстваЕГЭ (диагностич. работы)ЛогарифмыМетод рационализации

Диагностическая работа (декабрь 2013). Задание С3

Елена Репина 2013-12-13 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Рассмотрим С3 из Д/Р (без производной) от 12 декабря 2013 года.

Здесь можно посмотреть С3 из диагностической работы без логарифмов.

Решите систему неравенств:

$\begin{cases} 9^x-5\cdot 3^x+4\geq 0,\;(1)& &log_{\frac{3x^2+4x+1}{4x+1}}|\frac{x}{2}|\leq 0;\;(2) \end{cases}$

Решаем неравенство (1):

$9^x-5\cdot 3^x+4\geq 0;$

Неравенство – квадратное относительно $3^x.$ Находим дискриминант, раскладываем на множители:

$(3^x-1)(3^x-4)\geq 0;$

$3^x\leq 1$ или $3^x\geq 4;$

$3^x\leq 3^0$ или $3^x\geq 3^{\log_34};$

$x\leq 0$ или $x\geq log_34$

Итак, решение неравенства (1): $(-\infty;0]\cup [log_34;+\infty).$

Решаем неравенство (2):

$log_{\frac{3x^2+4x+1}{4x+1}}|\frac{x}{2}|\leq 0;$

$log_{\frac{3x^2+4x+1}{4x+1}}|\frac{x}{2}|\leq log_{\frac{3x^2+4x+1}{4x+1}}1;$

Далее применяем метод рационализации (на ОДЗ):

$\begin{cases} (\frac{3x^2+4x+1}{4x+1}-1)(|\frac{x}{2}|-1)\leq 0,& &\frac{3x^2+4x+1}{4x+1}>0,& &\frac{3x^2+4x+1}{4x+1}\neq 1,& &|\frac{x}{2}|>0; \end{cases}$

Множитель $|\frac{x}{2}|-1$ согласно, опять же, методу рационализации, заменяем на $(\frac{x}{2}-1)(\frac{x}{2}+1)$ :

$\begin{cases} (\frac{(3x^2+4x+1-4x-1)(\frac{x}{2}-1)(\frac{x}{2}+1)}{4x+1})\leq 0,& &3(x+1)(x+\frac{1}{3})(4x+1)>0,& &3x^2+4x+1\neq 4x+1,& &x\neq 0; \end{cases}$

$\begin{cases} \frac{x^2(x-2)(x+2)}{4x+1}\leq 0,& &(x+1)(x+\frac{1}{3})(4x+1)>0,& &x\neq 0; \end{cases}$

его

Итак, решение (2) неравнства: $(-\frac{1}{4};0)\cup (0;2].$

Пересекаем решения неравенств (1) и (2):

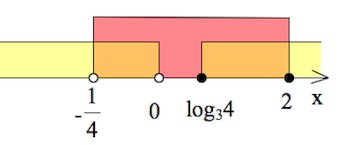
Ответ: $(-\frac{1}{4};0)\cup [log_34;2].$

Возможно, вам будет интересно аналогичное задание С3 смежного варианта:

+ показать

Автор: egeMax | комментария 3

Печать страницы

комментария 3

Ирина

2013-12-18 в 02:19

Елена Юрьевна, здравствуйте. Я ни в коем случаю не хочу Вас ткнуть носом, просто прикланяюсь перед Вашей оперативностью. А спешка в нашей работе, действительно иногда подводит. Посмотрите на координатную прямую в задании С3 от 12.12.2013 (без производной), там не все правильно. С уважением, Ирина.

[ Ответить ]
- egeMax
  
  2013-12-18 в 07:04
  
  Ирина, большое спасибо за отклик!
  Исправила! Было, конечно, круто… -1 правее -0,25… :)
  Видимо, была пятница, 13-го…
  
  [ Ответить ]
  - Ирина
    
    2013-12-23 в 02:19
    
    Бывает!!!!
    
    [ Ответить ]

Диагностическая работа (декабрь 2013). Задание С3

Добавить комментарий Отменить ответ