Диагностическая работа от 12 декабря 2013 года

В1. В розницу один номер еженедельного журнала «Репортаж» стоит 26 руб., а полугодовая подписка на этот журнал стоит 590 руб. За полгода выходит 25 номеров журнала. Сколько рублей сэкономит г-н Иванов за полгода, если не будет покупать каждый номер журнала отдельно, а оформит подписку?

Решение: + показать

B2. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

Решение: + показать

В3. На диаграмме показана средняя температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по верти- кали — средняя температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной средней температурой в 1994 году в Нижнем Новгороде.

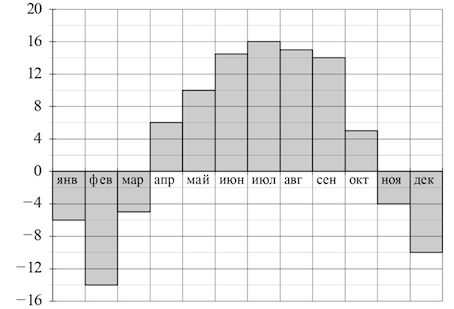
Решение: + показать

В4. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.

Определите, в каком из салонов покупка обойдётся дороже всего (с учётом переплаты), и в ответ напишите эту наибольшую сумму в рублях.

Решение: + показать

В5. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером 1см Х 1см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение: + показать

В6. В случайном эксперименте симметричную монету бросают четырежды.

Найдите вероятность того, что орёл выпадет ровно три раза.

Решение: + показать

В7. Найдите корень уравнения .

Решение: + показать

В8. В прямоугольном треугольнике угол между высотой и медианой, проведён- ными из вершины прямого угла, равен 28°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Решение: + показать

В9. На рисунке изображены график функции и касательная к нему

в точке с абсциссой . Найдите значение производной функции в точке .

Решение: + показать

В9. Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение: + показать

В11. Найдите значение выражения  .

Решение: + показать

В12. Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры: , где – постоянная, площадь S измеряется в квадратных метрах, а температура T – в градусах Кельвина. Известно, что некоторая звезда имеет площадь м , а излучаемая ею мощность P равна Вт. Определите температуру этой звезды. Ответ выразите в градусах Кельвина.

Решение: + показать

В13. В правильной треугольной пирамиде SABC точка K − середина ребра BC,  S − вершина. Известно, что AB = 6, а длина отрезка SK =7. Найдите площадь боковой поверхности пирамиды.

Решение: + показать

В14. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути   со  скоростью 50 км/ч, а вторую половину пути – со скоростью, на 15 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

Решение: + показать

В15. Найдите наименьшее значение функции на отрезке [−3; 3].

Решение: + показать

Смотрите также задания части С:
C1, С2, С3, С4, С5.

Также, возможно, вам будут интересны задания части В аналогичного варианта декабрьской диагностической работы (2013 г).