Дополнительный вступительный экзамен в МГУ, июль 2015

$f(2)=\frac{2}{5}+\frac{3}{2}+\frac{1}{10}=\frac{4+15+1}{10}=\frac{20}{10}=2.$

Ответ: $2.$ 

По теореме Виета $x_1\cdot x_2=5$ и $x_1+x_2=7,$ где $x_1,x_2$ – корни уравнения $x^2-7x+5=0.$

Тогда $x_1^2+x_2^2=(x_1+x_2)^2-2x_1\cdot x_2=49-10=39.$

Ответ: $39.$ 

$cosx+\sqrt2cos2x-sinx\geq 0;$

$cosx+\sqrt2(cosx-sinx)(cosx+sinx)-sinx\geq 0;$

$(cosx-sinx)(1+\sqrt2(cosx+sinx))\geq 0;$

Заметим,

$cosx+sinx=\sqrt2 (\frac{\sqrt2}{2}cosx+\frac{\sqrt2}{2}six)=\sqrt2(sin\frac{\pi}{4}cosx+cos\frac{\pi}{4}six)=$

$=\sqrt2sin(\frac{\pi}{4}+x)$

$cosx-sinx=\sqrt2 (\frac{\sqrt2}{2}cosx-\frac{\sqrt2}{2}sinx)=\sqrt2(sin\frac{\pi}{4}cosx-cos\frac{\pi}{4}six)=$

$=\sqrt2sin(\frac{\pi}{4}-x)=\sqrt{2}sin(\frac{\pi}{2}-(\frac{\pi}{4}+x))=\sqrt2cos(\frac{\pi}{4}+x).$

Поэтому переходим к следующему неравенству:

$\sqrt2cos(x+\frac{\pi}{4})(1+2sin(x+\frac{\pi}{4}))\geq 0;$

$cos(x+\frac{\pi}{4})(1+2sin(x+\frac{\pi}{4})\geq 0;$

$\begin{cases}cos(x+\frac{\pi}{4})\geq 0,\\1+2sin(x+\frac{\pi}{4})\geq 0;&\end{cases}$  или  $\begin{cases}cos(x+\frac{\pi}{4})\leq 0,\\1+2sin(x+\frac{\pi}{4})\leq 0;&\end{cases}$

$\begin{cases}cos(x+\frac{\pi}{4})\geq 0,\\sin(x+\frac{\pi}{4}))\geq -\frac{1}{2};&\end{cases}$  или  $\begin{cases}cos(x+\frac{\pi}{4})\leq 0,\\sin(x+\frac{\pi}{4})\leq -\frac{1}{2};&\end{cases}$

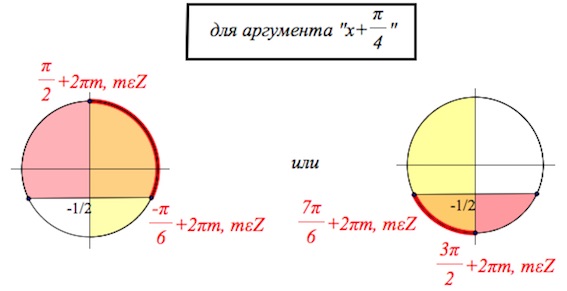
$x+\frac{\pi}{4}\in [-\frac{\pi}{6}+2\pi m;\frac{\pi}{2}+2\pi m]\cup [\frac{7\pi}{6}+2\pi m;\frac{3\pi}{2}+2\pim], m\in Z;$

Тогда

$x\in  [-\frac{5\pi}{12}+2\pi m;\frac{\pi}{4}+2\pi m]\cup [\frac{11\pi}{12}+2\pi m;\frac{5\pi}{4}+2\pi m], m\in Z.$

Ответ: $[-\frac{5\pi}{12}+2\pi m;\frac{\pi}{4}+2\pi m]\cup [\frac{11\pi}{12}+2\pi m;\frac{5\pi}{4}+2\pi m], m\in Z.$

$log_x|2x^2-3|=4log_{|2x^2-3|}x;$

$log_x|2x^2-3|=\frac{4}{log_x|2x^2-3|};$

$log^2_x|2x^2-3|=4$

$log_x|2x^2-3|=\pm 2;$

$log_x|2x^2-3|=log_xx^{\pm 2};$

$\begin{cases}\left[\begin{array}{rcl}|2x^2-3|=x^2,\\|2x^2-3|=\frac{1}{x^2};\end{array}\right.\\x\neq 1,\\x>0;\\2x^2-3\neq 0;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}x^2=3,\\x^2=1,\\2x^4-3x^2-1=0,\\2x^4-3x^2+1=0;\end{array}\right.\\x\neq 1,\\x>0;\\x^2\neq \frac{3}{2};&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}x=\pm \sqrt3,\\x=\pm 1,\\x^2=\frac{3\pm \sqrt{17}}{4},\\x^2=\frac{1}{2};\end{array}\right.\\x\neq 1,\\x>0;\\x^2\neq \frac{3}{2};&\end{cases}$

$\left[\begin{array}{rcl}x=\sqrt3,\\x=\frac{\sqrt{3+\sqrt{17}}}{2},\\x=\frac{\sqrt2}{2};\end{array}\right.$

Ответ: $\sqrt3,\frac{\sqrt{3+\sqrt{17}}}{2},\frac{\sqrt2}{2}.$

Пусть $K$ – середина $BC,$  $F$ – середина $AB,$ $O$ – центр данной окружности.

Заметим, в равнобедренном треугольнике $DOE$ медиана $FO$ является и высотой.

Итак, $OK,OF$ – серединные перпендикуляры к сторонам $BC,AB$ соответственно, то есть $O$ – центр окружности, описанной около треугольника $ABC.$

По свойству касательной и секущей, проведенных к окружности, $BK^2=BE\cdot BD,$  то есть, если обозначить $AB$ за $4x,$ то $BK^2=x\cdot 3x,$ откуда $BK=x\sqrt3.$

Так как по условию $\angle A=30^{\circ},$ то $\angle BOC=60^{\circ},$ то есть $\Delta BOC$ – равносторонний и $BO=2\sqrt3x.$ Тогда $OK=\frac{\sqrt3}{2}BO=3x.$ Но по условию $OK=\frac{3}{2},$ поэтому, очевидно, $x=\frac{1}{2}.$

По теореме косинусов для треугольника $ABC:$

$BC^2=AB^2+AC^2-4AB\cdot AC\cdot cos A;$

$3=4+AC^2-2\sqrt3AC;$

$AC^2-2\sqrt3AC+1=0;$

$AC=\sqrt3\pm \sqrt{2}.$

Ответ: $\sqrt3\pm \sqrt{2}.$

Поломка велосипеда Василия произошла на расстоянии $\frac{4}{3}$ км от А согласно условию.

За одно и тоже время, согласно условию, Василий и Георгий проделывают пути в $\frac{4}{3}$ и $4$ км соответственно. То есть их скорости отличаются втрое.

Пусть скорость Василия-пешехода – $x$ км/ч. Тогда скорость Георгия – $3x.$

Пусть встреча Василия с Георгием произошла на расстоянии $y$ от А. До встречи с Георгием Василий пройдет $\frac{4}{3}-y$ км, а Георгий  проедет $y$ км.

Тогда

$\frac{y}{3x}=\frac{\frac{4}{3}-y}{x};$

$\frac{y}{3}=\frac{4}{3}-y;$

$y=4-3y;$

$y=1.$

Ответ: $1.$

Пусть $K$ – центр основания $ABC$.

Заметим, $ED=a\sqrt3,$ если сторона основания – $3a$ и $AK$ – две трети высоты правильного треугольника со стороной $3a,$ то есть тоже $a\sqrt3.$ При этом, очевидно, $ED\parallel AK.$  $AEDK$ – параллелограмм, а значит, $DK\parallel AE.$

Прямая $AE$ параллельна плоскости $KDB$.

Поэтому

$\sqrt{13}=\rho (AE;BD)=\rho (AE;DBK)=\rho (A;DBK).$

Введем систему координат (xyz) так, как показано на рисунке.

Высота призмы – $2r,$ где $r$ – радиус вписанной в призму сферы.

Тогда $K(\frac{a\sqrt3}{2};0;0), B(0;\frac{3a}{2};0), D(0;\frac{a}{2};2r),A(\frac{3\sqrt3a}{2};0;0).$

Составим уравнение плоскости $DBK.$

$\begin{cases}A\cdot \frac{a\sqrt3}{2}+D=0,\\B\cdot \frac{3a}{2}+D=0,\\B\cdot \frac{a}{2}+C\cdot 2r+D=0;&\end{cases}$

$\begin{cases}D=-A\cdot \frac{a\sqrt3}{2},\\B=\frac{\sqrt3A}{3},\\C=A\cdot \frac{a\sqrt3}{6r};&\end{cases}$

Тогда уравнение плоскости $DBK$ есть

$A\cdot x+\frac{\sqrt3A}{3}\cdot y+A\cdot \frac{a\sqrt3}{6r}\cdot z-A\cdot \frac{a\sqrt3}{2}=0$

или

$x+\frac{\sqrt3}{3}\cdot y+\frac{a\sqrt3}{6r}\cdot z-\frac{a\sqrt3}{2}=0.$

Координаты вектора нормали плоскости $DBK$ – $(1;\frac{\sqrt3}{3};\frac{a\sqrt3}{6r}).$

Итак,

$\sqrt{13}=\frac{|\frac{3\sqrt3a}{2}-\frac{a\sqrt3}{2}|}{\sqrt{1^2+(\frac{\sqrt3}{3})^2+(\frac{a\sqrt3}{6r})^2}};$

$\sqrt{13}=\frac{a\sqrt3}{\sqrt{\frac{4}{3}+\frac{a^2}{12r^2}}};$

$13=\frac{3a^2}{\frac{4}{3}+\frac{a^2}{12r^2}};$

$\frac{52}{3}+\frac{13a^2}{12r^2}=3a^2.$

Но при этом $r=\frac{a\sqrt3}{2},$  откуда $a^2=\frac{4r^2}{3}.$

Потому

$\frac{52}{3}+\frac{13\cdot \frac{4r^2}{3}}{12r^2}=4r^2;$

$52\cdot 3+13=36r^2;$

$169=36 r^2;$

$r=\frac{13}{6}.$

Ответ: $\frac{13}{6}.$

Пусть

$4-3sin\alpha=a,$

$2+cos2\alpha=b,$

$\beta ^2+\beta+1=c,$

$\sqrt{\beta} +1=d.$

Замечаем, $a,b,c,d$ – положительные числа.

Воспользуемся при решении неравенством Коши: $x+y\geq 2\sqrt{xy}$ для $x,y\geq 0.$

$\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\geq 2\sqrt{\frac{a}{b}\cdot \frac{b}{c}}+2\sqrt{\frac{c}{d}\cdot \frac{d}{a}}=2(\sqrt{\frac{a}{c}}+\sqrt{\frac{c}{a}})\geq 2\cdot 2\sqrt{\sqrt{\frac{a}{c}}\cdot \sqrt{\frac{c}{a}}}=4.$

Равенство суммы $\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ четырем достигается при $a=b=c=d=1.$

Действительно, из $\frac{a}{b}+\frac{b}{c}=2\sqrt{\frac{a}{b}\cdot \frac{b}{c}}$ и $\frac{c}{d}+\frac{d}{a}=2\sqrt{\frac{c}{d}\cdot \frac{d}{a}}$ вытекает, что $\frac{a}{b}=\frac{b}{c}$ и $\frac{c}{d}=\frac{d}{a}$ соответственно.  Но тогда $ac=b^2=d^2,$ откуда $b=d.$

Далее, $\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}=\frac{a}{b}+\frac{b}{c}+\frac{c}{b}+\frac{b}{a}=4$. Становится видно, что, поскольку в последней сумме первое и последнее слагаемые, так же как и средние,  – взаимно обратные числа, а сумма положительных взаимно обратных чисел не меньше двух, то $a=b=c=d=1.$

$\begin{cases}4-3sin\alpha=2+cos2\alpha,\\\beta ^2+\beta+1=\sqrt{\beta} +1,\\\sqrt{\beta} +1=1;&\end{cases}$

$\begin{cases}sin\alpha =1,\\cos2\alpha =-1;\\\beta=0;&\end{cases}$

$\begin{cases}sin\alpha =1,\\\beta=0;&\end{cases}$

$\begin{cases}\alpha =\frac{\pi}{2}+2\pi n, n\in Z,\\\beta=0;&\end{cases}$

Итак, исходное выражение принимает свое минимальное значение при

$\alpha =\frac{\pi}{2}+2\pi n, n\in Z$,  $\beta=0.$

Ответ: $\alpha =\frac{\pi}{2}+2\pi n, n\in Z$,  $\beta=0.$