Досрочный вступительный экзамен в МГУ от 4 апреля 2015

$3x^3+x+26\geq 0;$

Замечаем, при $x=-2$   сумма $3x^3+x+26$ обращается в ноль.

Поэтому, так как

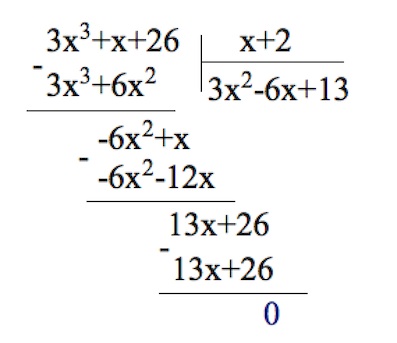
то имеем следующее неравенство:

$(x+2)(3x^2-6x+13)\geq 0;$

Второй множитель левой части неравенства  всегда положителен.

$x+2\geq 0;$

 Ответ: $[-2;+\infty).$ 

$2log_{1-|x-2|}|x-\frac{3}{2}|\leq 2;$

$log_{1-|x-2|}|x-\frac{3}{2}|}\leq log_{1-|x-2|}(1-|x-2|);$

Применяем метод замены множителей:

$\begin{cases}(1-|x-2|-1)(|x-\frac{3}{2}|-(1-|x-2|))\leq 0,\\1-|x-2|>0,\\1-|x-2|\neq 1,\\|x-\frac{3}{2}|\neq 0;&\end{cases}$
$\begin{cases}|x-2|(|x-\frac{3}{2}|-1+|x-2|)\geq 0,\\|x-2|<1,\\|x-2|\neq 0,\\x\neq \frac{3}{2};&\end{cases}$

$\begin{cases}|x-\frac{3}{2}|+|x-2|\geq 1,\\1<x<3,\\x\neq 2,\\x\neq \frac{3}{2};&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}\begin{cases}x<\frac{3}{2},\\-x+\frac{3}{2}-x+2\geq 1;\end{cases}\\\begin{cases}\frac{3}{2}<x<2,\\x-\frac{3}{2}-x+2\geq 1;\end{cases}\\\begin{cases}x>2,\\x-\frac{3}{2}+x-2\geq 1;\end{cases}\end{array}\right.\\1<x<3,\\x\neq 2,\\x\neq \frac{3}{2};&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}\begin{cases}x<\frac{3}{2},\\x\leq \frac{5}{4};\end{cases}\\\begin{cases}x>2,\\x\geq \frac{9}{4};\end{cases}\\\begin{cases}x>2,\\x-\frac{3}{2}+x-2\geq 1;\end{cases}\end{array}\right.\\1<x<3,\\x\neq 2,\\x\neq \frac{3}{2};&\end{cases}$

Ответ: $(1;1,25]\cup [2,25;3).$

$cos6x=sin4x, sin4x\neq 0;$

$cos6x=cos(\frac{\pi}{2}-4x),4x\neq \pi k, k\in Z;$

$\begin{cases}\left[\begin{array}{rcl}6x=\frac{\pi}{2}-4x+2\pi n, n\in Z,\\6x=-(\frac{\pi}{2}-4x)+2\pi n, n\in Z;\end{array}\right. \\x\neq \frac{\pi k}{4}, k\in Z;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}10x=\frac{\pi}{2}+2\pi n, n\in Z,\\2x=-\frac{\pi}{2}+2\pi n, n\in Z;\end{array}\right. \\x\neq \frac{\pi k}{4}, k\in Z;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}x=\frac{\pi}{20}+\frac{\pi n}{5}, n\in Z,\\x=-\frac{\pi}{4}+\pi n, n\in Z;\end{array}\right. \\x\neq \frac{\pi k}{4}, k\in Z;&\end{cases}$

Ответ: $\frac{\pi}{20}+\pi n;\frac{9\pi}{20}+\pi n;\frac{13\pi}{20}+\pi n;\frac{17\pi}{20}+\pi n,n\in Z.$

Заметим, $\frac{S_{ABD}}{S_{CBD}}=\frac{\frac{1}{2}AD\cdot h}{\frac{1}{2}DC\cdot h}=\frac{4}{3+3\sqrt3}.$

С другой стороны,  $\frac{S_{ABD}}{S_{CBD}}=\frac{\frac{1}{2}AB\cdot BD\cdot sin15^{\circ}}{\frac{1}{2}BC\cdot BD\cdot sin30^{\circ}}.$

Тогда

$\frac{AB}{2BC\cdot cos15^{\circ}}=\frac{4}{3+3\sqrt3}$   (*)

Пусть $CH\perp AB$  (заметим, $H$ может как принадлежать отрезку $AB$, так и не принадлежать ему). Рассмотрим оба случая.

Случай 1.

Пусть $BH=x$.

Очевидно, $CH=x$ и $BC=x\sqrt2.$

Равенство (*) примет следующий вид:

$\frac{x+AH}{2\sqrt2x\cdot cos15^{\circ}}=\frac{4}{3+3\sqrt3}.$

Далее

$AH=\frac{8\sqrt2x\cdot cos15^{\circ}}{3+3\sqrt3}-x;$

Итак,  $tgBAC=\frac{x}{AH}=\frac{1}{\frac{8\sqrt2\cdot cos15^{\circ}}{3+3\sqrt3}-1}.$

Так как $cos15^{\circ}=\frac{\sqrt{cos30^{\circ}+1}}{\sqrt2}=\sqrt{\frac{\frac{\sqrt3}{2}+1}{2}}=\sqrt{\frac{2\sqrt3+4}{8}}=\frac{\sqrt3+1}{2\sqrt2},$ то $tgBAC=\frac{1}{\frac{8\sqrt2\cdot \frac{\sqrt3+1}{2\sqrt2}}{3+3\sqrt3}-1}=\frac{3+3\sqrt3}{4\sqrt3+4-3-3\sqrt3}=3.$

Случай 2.

Пусть $BH=x$.

Очевидно, $CH=x$ и $BC=x\sqrt2.$

Равенство (*) примет следующий вид:

$\frac{x-AH}{2\sqrt2x\cdot cos15^{\circ}}=\frac{4}{3+3\sqrt3}.$

Далее

$AH=x-\frac{8\sqrt2x\cdot cos15^{\circ}}{3+3\sqrt3};$

$AH=x-\frac{8\sqrt2x\cdot \frac{1+\sqrt3}{2\sqrt2}}{3+3\sqrt3};$

$AH=x-\frac{4x}{\sqrt3}<0$ – случай 2 невозможен.

Ответ: 3.

Первый пловец проплывает дорожку за $\frac{50}{\frac{5}{12}}=120$ секунд ($2$ мин.), второй – за $\frac{50}{\frac{5}{11}}=110$ секунд ($\frac{11}{6}$ мин.).

Пусть первый пловец проплыл дорожку до встречи со вторым $n$ раз, на что у него ушло $2n$ минут. Тогда второй проплыл $n+1$ раз дорожку и на это у него ушло $\frac{11(n+1)}{6}$ минут.

Тогда первая встреча пловцов произошла через $22$ минуты, так как

$2n=\frac{11(n+1)}{6};$

$12n=11n+11;$

$n=11.$

Еще через $22$ минуты пловцов будет отделять одна дорожка (будут на противоположных сторонах бассейна).

Через следующие $22$ минуты, то есть после $66$ минут после старта пловцы окажутся вновь на одной из сторон бассейна.

Следующая встреча на одной из сторон бассейна произошла бы через $110$ минут после старта, но друзья плавали $90$ минут.

Итак, через $66$ минут после старта второй пловец последний раз догонит первого точно у одной из сторон бассейна.

Ответ: 66.

$\sqrt{a-|x-3a|}\leq a-|x-3a|;$

$\begin{cases}a-|x-3a|\leq (a-|x-3a|)^2,\\a-|x-3a|\geq 0;&\end{cases}$

$\begin{cases}(a-|x-3a|) (1-a+|x-3a|)\leq 0,\\a-|x-3a|\geq 0;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}a-|x-3a|\leq 0,\\a-|x-3a|\geq 1;\end{array}\right. \\a-|x-3a|\geq 0;&\end{cases}$

Ответ: 3.

Расстояние между  $AB_1$ и $A_1D$ есть расстояние между $AB_1$ и $A_1C_1D$ (так как $AB_1\parallel A_1C_1D$).

А расстояние от $AB_1$  до $A_1C_1D$ – длина высоты $H$ пирамиды $AA_1C_1D$ с основанием $A_1C_1D.$

$H=\frac{3V_{AA_1C_1D}}{S_{A_1C_1D}}=\frac{3\cdot \frac{1}{3}\cdot S_{AA_1D}\cdot C_1D_1}{S_{A_1C_1D}}=\frac{3}{S_{A_1C_1D}}.$

По т. косинусов для треугольника $A_1C_1D$:

$A_1D^2=A_1C_1^2+DC_1^2-2A_1C_1\cdot DC_1cosC_1;$

$13=10+5-10\sqrt2cosC_1;$

$cosC_1=\frac{1}{5\sqrt2}.$

Тогда

$sinC_1=\sqrt{1-(\frac{1}{5\sqrt2})^2}=\frac{7}{5\sqrt2}.$

Стало быть, $S_{A_1C_1D}=\frac{1}{2}\cdot A_1C_1\cdot DC_1\cdot sinC_1=\frac{7}{2}.$

Наконец, $H=\frac{3}{\frac{7}{2}}=\frac{6}{7}.$

Ответ: $\frac{6}{7}.$