Главная › Справочные материалы › Формула длины биссектрисы через длины сторон треугольника

24 Ноя 2015

Категория: Справочные материалы

Формула длины биссектрисы через длины сторон треугольника

Елена Репина 2015-11-24 2016-07-10

Докажем следующую теорему.

Пусть $a,b,c$ – стороны треугольника, $l_a$ – биссектриса треугольника проведенная к стороне $a$ .

Тогда

$l_a=\frac{\sqrt{bc(a+b+c)(b+c-a)}}{b+c}.$

Доказательство:

Пусть $AL=l_a$ – биссектриса треугольника $ABC.$

Пусть $BL=c_1,CL=b_1.$ Пусть $\angle A=2\alpha.$

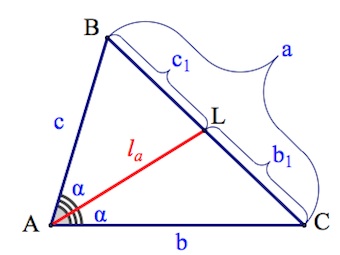
Распишем теорему Косинусов для треугольников $ABL,ACL:$

$c_1^2=c^2+l_a^2-2cl_acos\alpha;$

$b_1^2=b^2+l_a^2-2bl_acos\alpha;$

Откуда

$\frac{c^2+l_a^2-c_1^2}{2cl_a}=\frac{b^2+l_2^2-b_1^2}{2bl_a}$ (1)

По свойству биссектрисы треугольника

$\frac{c}{c_1}=\frac{b}{b_1}.$

Или

$\frac{c}{c_1}=\frac{b}{a-c_1}.$

Откуда

$c_1=\frac{ac}{b+c}$ (2)

Тогда

$b_1=a-\frac{ac}{b+c}=\frac{ab}{b+c}$ (3)

Подставляем (2) и (3) в (1):

$\frac{c^2+l_a^2-(\frac{ac}{b+c})^2}{2cl_a}=\frac{b^2+l_a^2-(\frac{ab}{b+c})^2}{2bl_a};$

$b(c^2+l_a^2-(\frac{ac}{b+c})^2)=c(b^2+l_a^2-(\frac{ab}{b+c})^2);$

$l_a^2(b-c)=cb^2+b(\frac{ac}{b+c})^2-bc^2-c(\frac{ab}{b+c})^2);$

$l_a^2(b-c)=\frac{cb^2(b+c)^2+a^2bc^2-bc^2(b+c)^2-a^2b^2c}{(b+c)^2};$

$l_a^2=\frac{bc(b+c)^2(b-c)-a^2bc(b-c)}{(b-c)(b+c)^2};$

$l_a^2=\frac{bc(b-c)((b+c)^2-a^2)}{(b-c)(b+c)^2};$

$l_a^2=\frac{bc(b+c-a)(a+b+c)}{(b+c)^2};$

$l_a=\frac{\sqrt{bc(a+b+c)(b+c-a)}}{b+c}.$

Что и требовалось доказать.

Автор: egeMax | комментариев 5

Печать страницы

комментариев 5

Елена

2015-11-25 в 20:49

Елена, спасибо огромное за данный материал! В нашем регионе (Рязань) на районных олимпиадах дают задания на доказательство некоторых утверждений, которые используются в С4 ЕГЭ. Это одна из таких задач. Будем работать с учениками. С уважением, Елена.

[ Ответить ]
- egeMax
  
  2015-11-25 в 22:35
  
  ;)
  
  [ Ответить ]
Мария

2015-11-26 в 18:32

Спасибо. Хорошее доказательство, и главное всё понятно. Толь во второй строчке исправьте цифру 2 на а

[ Ответить ]
- egeMax
  
  2015-11-26 в 19:47
  
  Мария, спасибо.
  
  [ Ответить ]
ака

2022-10-16 в 13:53

как можно так резко без объяснения переходить к следующему выражению

[ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (34)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (94)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы