Главная / Тригонометрические выражения, уравнения и неравенства

01 Июл 2013

Категория: Тригонометрические выражения, уравнения и неравенства

Формулы для решения простейших тригонометрических уравнений. Часть 2

Елена Репина 2013-07-01 2013-10-23

Мы уже говорили о том, что все тригонометрические уравнения сводятся к решению четырех основных типов простейших уравнений.

В части 1 статьи мы научились решать уравнения вида $cos\:x=a$ .

Сейчас займемся решением уравнений вида $sin\:x=a$ .

В 3-й части статьи смотрите решение уравнений вида $tg\:x=a,\;ctg\:x=a$ .

Уравнение вида $\LARGE sin\:x=a$

Решим уравнение $sin\:x=\frac{1}{2}$ .

Находим на оси синусов на тригонометрическом круге $\frac{1}{2}$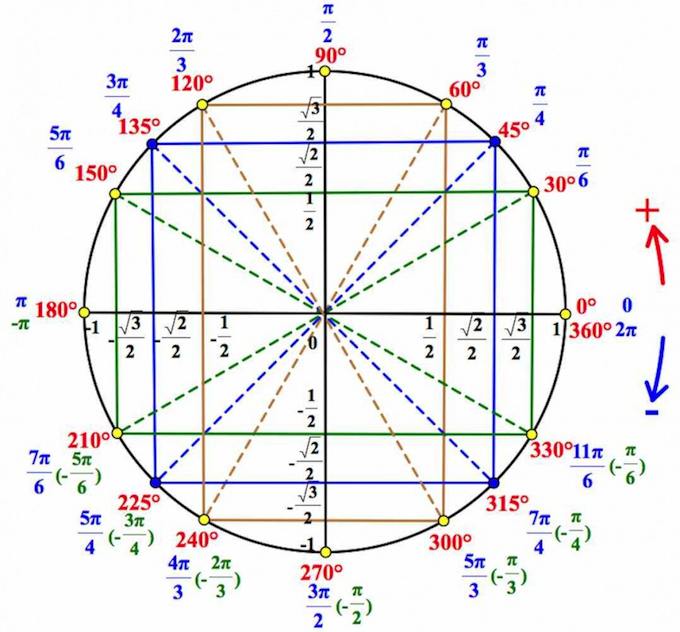 : 87yhjh

Проводя горизонталь через точку $\frac{1}{2}$ оси синусов, выходим на точки круга $\frac{\pi}{6}$ и $\frac{5\pi}{6}$ :

решение тригонометрического уравнения на круге

Как мы знаем, за каждой из полученных точек скрывается бесконечно много других точек. Например, точка $\frac{\pi}{6}+2\pi$ на тригонометрическом круге располагается там же, где и $\frac{\pi}{6}$ , значит значение синуса в этой точке также равно $\frac{1}{2}$ .

На оси подходящие нам точки располагаются так:

радианы на оси

Графическое решение уравнения $sin\:x=\frac{1}{2}$ :

графическое решение уравнения sin x =0.5

Мы уже знаем, что все подходящие точки взять в ответ нам позволяет счетчик. То есть мы вводим целое число $n$

( $n=...,\;-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;...$ ).

И записываем ответ так:

$x=\frac{\pi}{6}+2\pi n,\;n\in Z$ или $x=\frac{5\pi}{6}+2\pi n,\;n\in Z$

Эти две серии решений можно записать и в одну строку:

$x=(-1)^n\frac{\pi}{6}+\pi n,\;n\in Z$

Поперебирайте различные значения $n$ , и вы убедитесь, что все нужные нам точки укладываются в эту формулу.

И все же,

…

$n=-1:$ $x=-\frac{\pi}{6}-\pi$ , то есть $x=-\frac{7\pi}{6};$

$n=0:$ $x=\frac{\pi}{6};$

$n=1:$ $x=-\frac{\pi}{6}+\pi$ , то есть $x=\frac{5\pi}{6};$

$n=2:$ $x=\frac{\pi}{6}+2\pi$ , то есть $x=\frac{13\pi}{6};$

и т.д.

Убедились?

Если бы мы решали, например, уравнение $sin\:x=-\frac{\sqrt2}{2}$ ,

тригонометрия на круге

то решением бы было

$x_1=-\frac{\pi}{4}+2\pi n,\;x_2=-\frac{3\pi}{4}+2\pi n,\;n\in Z$

или, что тоже самое,

$x=(-1)^{n}\cdot (-\frac{\pi}{4})+\pi n,n\in Z,$

то есть $x=(-1)^{n+1}\frac{\pi}{4}+\pi n,n\in Z.$

Я думаю, вы уже увидели общий принцип формирования ответа.

Давайте дадим формулу, которой можно руководствоваться, решая уравнения

$sin\:x=a$ , где $a$ – из $[-1;\:1]$

(в противном случае, когда $a$ – не из $[-1;\;1]$ – решений нет)

Но вам формула будет понятна, если вы уже знакомы с понятием «арксинус».

$x=(-1)^n arcsin\:a +\pi n, \;n\in Z$

или, что тоже самое

$x_1= arcsin\:a +2\pi n, \;x_2=\pi-arcsin\:a+2\pi n,\;n\in Z$

Если нам встречается уравнение с нетабличным значением синуса, вроде этого $sin\:x=-\frac{1}{5}$ , то ответ будет выглядеть так:

$x=(-1)^narcsin(-\frac{1}{5})+\pi n,\;n\in Z,$

то есть $x=(-1)^{n+1}arcsin\frac{1}{5}+\pi n,\;n\in Z$

(согласно свойству функции арксинус).

Частные случаи решения уравнения $sin\:x=a$

1) $sin\:x=0$

частные случаи простейших тригонометрических уравнений

Ответ прекрасно ложится в одну строку без всяких там $(-1)^n$ за счет полукругового счетчика $\pi n$ .

Имеем: $x=\pi n,\;n\in Z.$

2) $sin \:x=1$

частный случай sin x=a

У нас всего одна серия точек: $x=\frac{\pi}{2}+2\pi n,\;n\in Z.$

3) $sin \:x=-1$

sinx=-1

Аналогично примеру 2 имеем: $x=-\frac{\pi}{2}+2\pi n,\;n\in Z.$

Автор: egeMax | Один комментарий

Печать страницы

Один комментарий

Бексултан

2016-12-19 в 19:21

Спасибо,вам в целом.Подаваемая вами информация проста в усвоении(еще раз повторюсь) спасибо вам большое))!! Удачи в дальнейшем развитии сайта.Надеюсь скоро появится больше статей для любознательных школьников и абитуриентов))

[ Ответить ]

Формулы для решения простейших тригонометрических уравнений. Часть 2

Уравнение вида

Добавить комментарий Отменить ответ

Уравнение вида $\LARGE sin\:x=a$