Главная
Справочник
Видеоуроки
Тесты
Статьи
Архив
Карта сайта
Контакты
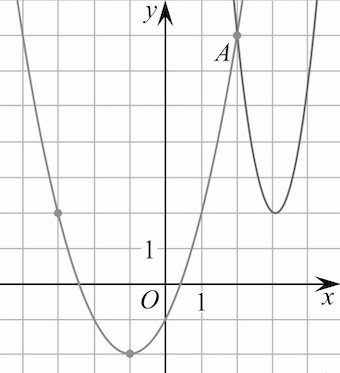
Задача 1. На рисунке изображены графики функций 
и 
которые пересекаются в точках 
и 
Найдите ординату точки
Решение: + показать
– правый график, так как свободный член 
в формуле указывает на пересечение графика с осью ординат в точке 
откуда, кстати, вытекает, что 
, значит 
проходит, например, через точку 
Тогда 
или 
– это 
Тогда ордината: 
Задача 2. На рисунке изображён график функции вида 
где числа 
и 
— целые. Найдите значение 
Решение: + показать
Задача 3. На рисунке изображён график функции вида 
где числа и — целые. Найдите значение дискриминанта уравнения 
Решение: + показать
выглядит так:
Задача 4. На рисунке изображён график функции вида где числа и — целые. Найдите абсциссу вершины параболы.
Решение: + показать
Вы можете пройти тест: “Параболы”
Добавить комментарий