Иррациональные неравенства

Какая информация заложена в самом неравенстве?

$x^2+5x\geq 0$ и $1-x^2+4x\geq 0$, верно? Ведь подкоренное  выражение не может быть отрицательным (имеется ввиду корень четной кратности).

Мы сохраним эту информацию.

Неравенство равносильно системе:

$\begin{cases} x^2+5x<1-x^2+4x,\\x^2+5x\geq 0; \end{cases}$

Обратите внимание, – нет необходимости указывать и $1-x^2+4x\geq 0$! Ведь об этом уже сказано в системе.

$\begin{cases} 2x^2+x-1<0,\\x(x+5)\geq 0; \end{cases}$
$\begin{cases}2(x-0,5)(x+1)<0,\\x(x+5)\geq 0;\end{cases}$

Каждое неравенство системы решаем методом интервалов:

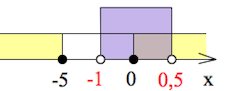
Итак,

$x\in [0;\;0,5)$.

Ответ: $[0;\;0,5)$ 

Обе части неравенства – неотрицательны. Возведем в квадрат обе части, перейдем к системе, равносильной исходному неравенству:

$\begin{cases}x^2-3x-10<(8-x)^2,\\8-x\geq 0,\\x^2-3x-10\geq 0;&\end{cases}$

$\begin{cases}x^2-3x-10<64-16x+x^2,\\x\leq  8,\\(x-5)(x+2)\geq 0;&\end{cases}$

Из первых двух неравенств системы остается одно – первое (его решение является пересечение множеств решений указанных двух неравенств).

$\begin{cases}x<\frac{74}{13},\\(x-5)(x+2)\geq 0;&\end{cases}$

$x\in(-\infty;-2]\cup [5;\frac{74}{13}).$

Ответ: $(-\infty;-2]\cup [5;\frac{74}{13}).$ 

Правая часть неравенства может быть как отрицательной, так и неотрицательной. Мы не можем просто так взять и возвести обе части неравенства в квадрат.

Будем рассматривать два случая:

1) $x+2\geq 0$

Тогда мы можем возвести обе части в квадрат и перейти к системе:

$\begin{cases}x+2\geq 0,\\x^2-5x-24>(x+2)^2;\end{cases}$

2) $x+2<0$

Тогда мы видим следующее:

Правая часть неравенства (всегда неотрицательная величина) больше отрицательной величины. Это верно.

То есть мы получаем верное неравенство на области его определения $(x^2-5x-24\geq 0).$

Значит, перед нами система:

$\begin{cases}x+2<0,\\x^2-5x-24\geq 0;&\end{cases}$

Проще говоря, будем решать совокупность двух систем:

$\left[\begin{array}{rcl}\begin{cases}x+2\geq 0,\\x^2-5x-24>(x+2)^2;\end{cases}\\\begin{cases}x+2<0,\\x^2-5x-24\geq 0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}x\geq -2,\\x^2-5x-24>x^2+4x+4;\end{cases}\\\begin{cases}x<-2,\\(x-8)(x+3)\geq 0 ;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}x\geq -2,\\x<-\frac{28}{9};\end{cases}\\\begin{cases}x<-2,\\(x-8)(x+3)\geq 0 ;\end{cases}\end{array}\right.$

Первая система решений не имеет:

А решение второй системы графически выглядит так:

Поэтому

$x\in (-\infty;-3].$

Ответ: $(-\infty;-3].$ 

Перепишем неравенство вот так:

$(x+1)\sqrt{x^2+1}>(x-1)(x+1);$

Мы должны четко понимать, что нельзя обе части неравенства поделить на $x+1$! Мы же не знаем знак этой суммы.

Выход такой – вынесение за скобку общего множителя:

$(x+1)(\sqrt{x^2+1}-(x-1))>0;$

Тогда неравенство равносильно совокупности двух систем:

$\left[\begin{array}{rcl}\begin{cases}x+1>0,\\\sqrt{x^2+1}>x-1;\end{cases}\\\begin{cases}x+1<0,\\\sqrt{x^2+1}<x-1;\end{cases}\end{array}\right.$

Второе неравенство первой системы $\sqrt{x^2+1}>x-1$ равносильно совокупности:

$\left[\begin{array}{rcl}\begin{cases}x-1\geq 0,\\x^2+1>(x-1)^2;\end{cases}\\\begin{cases}x-1<0,\\\sqrt{x^2+1}<x-1;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}x\geq 1,\\x>0;\end{cases}\\x<1;\end{array}\right.$

$\left[\begin{array}{rcl}x\geq 1,\\x<1;\end{array}\right.$

То есть решение данного неравенства – $x\in R.$

Второе неравенство второй системы указанной выше совокупности $\sqrt{x^2+1}<x-1$ равносильно  системе:

$\begin{cases}x\geq 1,\\x^2+1<(x-1)^2;&\end{cases}$

Откуда

$\begin{cases}x\geq 1,\\x<0;&\end{cases}$

То есть система не имеет решений.

Возвращаемся в совокупность, которая равносильна исходному неравенству, получаем:

$x\in (-1;+\infty)$.

Ответ: $(-1;+\infty)$. 

Как и в предыдущем задании выносим общий множитель за скобку:

$\sqrt{6+x-x^2}(\frac{1}{2x+5}-\frac{1}{x+4})\geq 0;$

$\sqrt{6+x-x^2}\cdot \frac{x+4-2x-5}{(2x+5)(x+4)}\geq 0;$

$\sqrt{6+x-x^2}\cdot \frac{-x-1}{(2x+5)(x+4)}\geq 0;$

или (после домножения на -1 обеих частей):

$\sqrt{6+x-x^2}\cdot \frac{x+1}{(2x+5)(x+4)}\leq 0;$

Перепишем неравенство так:

$(\sqrt{6+x-x^2}-\sqrt0)\cdot \frac{x+1}{(2x+5)(x+4)}\leq 0$

и применим метод рационализации:

$\begin{cases}(6+x-x^2)\cdot \frac{x+1}{(2x+5)(x+4)}\leq 0,\\6+x-x^2\geq 0;&\end{cases}$

$\begin{cases}\frac{(x+1)\cdot (x^2-x-6)}{(2x+5)(x+4)}\geq 0,\\x^2-x-6\leq 0;&\end{cases}$

$\begin{cases}\frac{(x+1)\cdot (x-3)(x+2)}{(2x+5)(x+4)}\geq 0,\\(x-3)(x+2)\leq 0;&\end{cases}$

$x\in[-2;-1]\cup ${$3$}.

Ответ: $[-2;-1]\cup ${$3$}. 

Данное неравенство равносильно следующему:

$x+2\sqrt{x}\sqrt{x-5}+x-5\leq 10-x;$

$2\sqrt{x}\sqrt{x-5}\leq 15-3x;$

$\begin{cases}4x\cdot (x-5)\leq (15-3x)^2,\\15-3x\geq 0,\\x\geq 5;\end{cases}$

$\begin{cases}4x\cdot (x-5)\leq (15-3x)^2,\\x\leq 5,\\x\geq 5;\end{cases}$

Очевидно, что в ответ если из системы какой $x$  и попадет, то это может быть только $5$.

Проверим, удовлетворяет ли $5$ первому неравенству системы.

Ответ очевиден, – да.

Ответ: $5.$ 

$\sqrt{4x^2+x+9}>3-\sqrt{4x^2+x};$

$\left[\begin{array}{rcl}\begin{cases}3-\sqrt{4x^2+x}\geq 0,\\4x^2+x+9>9-6\sqrt{4x^2+x}+4x^2+x;\end{cases}\\\begin{cases}3-\sqrt{4x^2+x}<0,\\4x^2+x+9\geq 0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}3\geq \sqrt{4x^2+x},\\\sqrt{4x^2+x}>0;\end{cases}\\\begin{cases}3<\sqrt{4x^2+x},\\x\in R;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}4x^2+x\leq 9,\\x(4x+1)>0;\end{cases}\\\begin{cases}4x^2+x>9,\\x\in R;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}4(x-\frac{1-\sqrt{145}}{8})(x-\frac{1+\sqrt{145}}{8})\leq 0,\\x(4x+1)>0;\end{cases}\\\begin{cases}4(x-\frac{1-\sqrt{145}}{8})(x-\frac{1+\sqrt{145}}{8})>0,\\x\in R;\end{cases}\end{array}\right.$

Графическое решение первой системы:

Графическое решение второй системы:

Объединяя решения, получаем:

$x\in (-\infty;-\frac{1}{4})\cup(0;+\infty).$

Ответ: $(-\infty;-\frac{1}{4})\cup(0;+\infty).$