25 Фев 2014

Категория: Справочные материалы

Коллекционерам формул посвящается

Елена Репина 2014-02-25 2014-03-05

Вы считаете, что чем больше формул знаете, тем спокойнее на экзамене? Так-то оно так, но в случае, если вы дейтвительно понимаете суть формул.

Но если вы коллекционируете формулы, не особо разбираясь в них, не видя связей, следствий, то вряд ли это вас спасет…

Давайте вот прямо сейчас выкинем ряд «лишних» формул из ваших шпаргалок!

Выкидываем из шпаргалки формулу площади правильного треугольника

Наверняка в вашей коллекции есть формула площади правильного треугольника $S=\frac{a^2\sqrt3}{4}.$ Если вы ее знаете, – рада за вас, если нет, – давайте поймем как ее в два счета вывести.

Вы обязаны знать формулу площади $S=\frac{1}{2}absin\gamma$ для треугольника со сторонами $a,\;b$ и углом между ними $\gamma.$

А в правильном треугольнике $a=b$ и $sin\gamma=sin60^{\circ}=\frac{\sqrt3}{2}.$ Вот и получаем требуемую формулу: $S=\frac{a^2\sqrt3}{4}.$

Много времени занял вывод формулы?

Выкидываем из шпаргалки формулу площади сектора

$S_{sektor}=\frac{\alpha \pi R^2}{360^{\circ}}$

Составим пропорцию

Площадь сектора в $360^{\circ}$ (круга) – $\pi R^2$ , какая площадь будет у сектора в $\alpha$ градусов находим через пропорцию. Отсюда сразу и получаем формулу.

А в принципе, она и не нужна вовсе… Просто в каждой конкретной задаче вы составляете свою пропорцию.

Например, нужно решить следующую задачу: –> + показать

Выкидываем пару формул из таблицы производных

Наверняка, в таблице производных у вас есть такие две строки:

Вы знаете формулу $(x^{\alpha})'=\alpha x^{\alpha-1}$ , где $\alpha$ – действительное число.

Так разве $\sqrt{x}$ – это не $x^{\frac{1}{2}}$ ?

$(x^{\frac{1}{2}})'=\frac{1}{2}x^{\frac{1}{2}-1}=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2x^{\frac{1}{2}}}=\frac{1}{2\sqrt{x}}.$

Аналогично $(\frac{1}{x})'=(x^{-1})'=-1\cdot x^{-2}=-\frac{1}{x^2}.$

Кстати, + показать

Выкидываем из шпаргалки формулу боковой поверхности цилиндра

Формула боковой поверхности цилиндра

$S=2\pi RH$

(где $R,\;H$ – радиус и высота цилиндра соответственно)

вполне может встретиться в задачах ЕГЭ по математике.

Но ведь что есть боковая поверхность цилиндра в развертке?

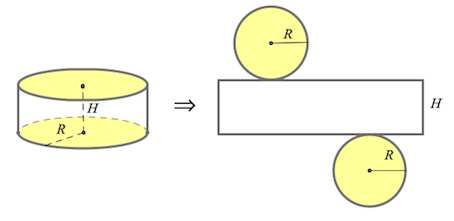
Это прямоугольник с одной стороной – $H$ , второй стороной, равной длине окружности основания, то есть $2\pi R.$

Потому и получаем

$S=2\pi RH.$

Выкидываем теорему Пифагора

Шучу, конечно, – кто не знает теорему Пифагора? Но может быть, вам сложно выучить теорему косинусов? Вы подозревали раньше, что теорема Пифагора – частный случай теоремы косинусов?

$c^2=a^2+b^2-2abcos\gamma$

А ведь в случае прямого угла $C$ косинус его будет равен 0, а следовательно, мы и получим теорему Пифагора: $c^2=a^2+b^2.$

Выкидываем из шпаргалок несколько тригонометрических формул

Не обойтись на ЕГЭ по математике без формул двойного угла для косинуса:

$cos2\alpha=cos^2\alpha-sin^2\alpha$

$cos2\alpha=2cos^2\alpha-1$

$cos2\alpha=1-2sin^2\alpha$

Так вот две последние формулы запоминать нет никакой необходимости. Посмотрите, как быстро выводится, например, средняя формула:

$cos2\alpha=cos^2\alpha-sin^2\alpha=cos^2\alpha-(1-cos^2\alpha)=2cos^2\alpha-1.$

С третьей формулой – аналогично.

Анализируем формулу площади четырехугольника через диагонали

Хорошо бы знать формулу площади четырехугольника с диагоналями $d_1,\;d_2$ и углом между ними $\alpha$ …

$S=\frac{d_1d_2sin\alpha}{2}$

Тогда набор формул

$S=\frac{d^2}{2}$ для квадрата с диагональю $d$ ,

$S=\frac{d^2sin\alpha}{2}$ для прямоугольника с диагоналями $d$ и углом $\alpha$ между ними,

$S=\frac{d_1d_2}{2}$ для ромба с диагоналями $d_1,\;d_2$

не придется запоминать!

Становится ясно, что это всего лишь частные случаи формулы $S=\frac{d_1d_2sin\alpha}{2}$ (например, в квадрате $d_1=d_2$ и $\sin\alpha=1$ , так как $\alpha=90^{\circ}$ ).

Рада, если описанные случаи для вас очевидны –> ;) + показать

Значит, вы хорошо подготовлены к ЕГЭ по математике (по крайней мере, к части В)!

Можно продолжать и далее…

Но пока все! Вам есть что сказать/спросить? Пишите в комментариях.

стрелка вниз

Автор: egeMax | комментариев 18

Печать страницы

комментариев 18

Анатолий Шевелев

2014-02-25 в 12:37

“cos\alpha=cos^2\alpha-sin^2\alpha” может вы хотели сказать “cos2A”

[ Ответить ]
- egeMax
  
  2014-02-25 в 12:49
  
  Да, да, спасибо!
  
  [ Ответить ]
Анатолий Шевелев

2014-02-25 в 12:45

хорошо если статья будет постепенно пополняться новыми заметками :)

[ Ответить ]
- egeMax
  
  2014-02-25 в 13:02
  
  Если это интересно, то будет ;)
  
  [ Ответить ]
  - Анатолий Шевелев
    
    2014-02-25 в 13:04
    
    Конечно интересно ;)
    
    [ Ответить ]
egetrener

2014-02-25 в 14:05

Елена Юрьевна, класс! Мы с Вами очень близки по духу. Формулы – зло))

[ Ответить ]
- egeMax
  
  2014-02-25 в 14:46
  
  Ольга Игоревна, приятно слышать!
  Да уж, многие так и теряются в формулах, не доходя до решения задачи…
  
  [ Ответить ]
Галина Михайловна

2014-02-25 в 14:22

Спасибо. Идея хорошая.

[ Ответить ]
Элла

2014-02-26 в 00:08

Вот эта солидарность!!! Я тоже в своей работе не заставляю детей заучивать именно те формулы, которые можно “выкинуть”.

[ Ответить ]
- egeMax
  
  2014-02-26 в 00:12
  
  Наши ряды «нелюбителей формул» пополняются! :D
  
  [ Ответить ]
  - Ирина
    
    2014-02-26 в 03:48
    
    Елена, а я с Вами во ВСЁМ!!! Хотя иногда мы с Вами подходим по разному к решению одной и т.ж. задачи. Но это нормально.
    
    [ Ответить ]
Надежда

2014-02-26 в 15:42

Елена Юрьевна, я с Вами полностью согласна и ученики мои не запоминают перечисленные формулы.

[ Ответить ]
- egeMax
  
  2014-02-26 в 19:26
  
  :)
  
  [ Ответить ]
Иванов

2014-03-03 в 18:54

Знание формул без их понимания это как знание текста рассказа наизусть, но абсолютного непонимания его:)

[ Ответить ]
- egeMax
  
  2014-03-03 в 20:15
  
  Точно! :D
  
  [ Ответить ]
Анатолий Шевелев

2014-04-22 в 10:47

хорошо бы описать поведение формулы $S=\frac{1}{2}absin\gamma$ с различными многоугольниками (треугольник, квадрат, параллелограмм и т.д.)

[ Ответить ]
Kirill

2017-05-19 в 01:23

Я думал тут будет 555 формул по тригонометрии=)))(, из которых только 55 изучаются в школе!=)

[ Ответить ]
- egeMax
  
  2017-05-19 в 11:34
  
  [ Ответить ]