Метод интервалов для дробно-рациональных неравенств. Часть 2.

Неравенство $\frac{x-2}{3x+5}\leq 0$ равносильно следующей системе:

$\begin{cases}
(x-2)(3x+5)\leq 0,
\\3x+5\neq 0;
\end{cases}$

Решаем исходное неравенство как обычное рациональное неравенство, при этом обязательно «выкалываем» точку $x=-\frac{5}{3}$.

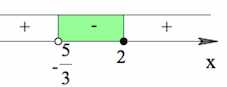
Ответ: $(-\frac{5}{3};2]$. 

Исходное неравенство равносильно следующему:

$(x-4)(x-3)(3x-7-x^2)(x^2+x-2)>0$

Разложим на множители последнюю скобку неравенства:

$x^2+x-2=(x-1)(x+2)$ (пользуясь п.7).

А вот  квадратный трехчлен $(3x-7-x^2)$ на множители не раскладывается, так как $D<0$.

Это означает, что выражение принимает только знак «-». Действительно, возьмите любое число, например, 0, подставьте в $(3x-7-x^2)$, –  получите -7. А сменить этот знак квадратному трехчлену на другой просто негде – нулей-то нет.

Поэтому, мы можем сократить обе части исходного неравенства на отрицательную величину $(3x-7-x^2)$, при этом поменяв знак неравенства на $<$.

Итак, решаем следующее неравенство

$(x-4)(x-3)(x-1)(x+2)<0$, равносильное исходному.

Ответ: $(-2;1)\cup(3;4)$. 

Исходное неравенство равносильно следующей системе:

$\begin{cases}
(x^3+5x-6)(x+2)\geq 0,
\\x+2\neq 0;
\end{cases}$

Заметим,

$x^3+5x-6=x^3-x+6x-6=x(x^2-1)+6(x-1)=$

$=x(x-1)(x+1)+6(x-1)=(x-1)(x^2+x+6)$

При этом $x^2+x+6>0$ на R.

То есть исходное неравенство равносильно следующему (сократили обе части на $x^2+x+6$):

$(x-1)(x+2)\geq 0$ при условии, что $x+2\neq 0$.

Поэтому

Ответ:  $(-\infty;-2)\cup[1;+\infty)$. 

Первое, что необходимо сделать – перенести $\frac{1}{2}$ влево и привести к общему знаменателю:

$\frac{2x+3}{x^2+x-12}-\frac{1}{2}\leq 0$

$\frac{2(2x+3)-(x^2+x-12)}{2(x^2+x-12)}\leq 0$

$\frac{4x+6-x^2-x+12}{2(x^2+x-12)}\leq 0$

$\frac{-x^2+3x+18}{2(x^2+x-12)}\leq 0$

Домножим обе части неравенства на -1, поменяв при этом знак неравенства:

$\frac{x^2-3x-18}{2(x^2+x-12)}\geq 0$

Исходное неравенство равносильно следующей системе:

$\begin{cases}
(x^2-3x-18)(x^2+x-12)\geq 0,
\\x^2+x-12\neq 0;
\end{cases}$

Далее, после разложения на множители, имеем:

$\begin{cases}
(x-6)(x+3)(x-3)(x+4)\geq 0,
\\(x-3)(x+4)\neq 0;
\end{cases}$

Ответ: $(-\infty;-4)\cup[-3;3)\cup[6;+\infty)$. 

Первое, что необходимо сделать – перенести $\frac{1}{x}$ влево и привести  все три дроби к общему знаменателю:

$\frac{x(x-1)+x(x-2)-(x-2)(x-1)}{(x-2)(x-1)x}\geq 0$

Производим преобразования:

$\frac{x^2-x+x^2-2x-x^2+3x-2}{(x-2)(x-1)x}\geq 0$

$\frac{x^2-2}{(x-2)(x-1)x}\geq 0$

Исходное неравенство равносильно следующей системе:

$\begin{cases}
(x^2-2)(x-2)(x-1)x\geq 0,
\\(x-2)(x-1)x\neq 0;
\end{cases}$

После разложения на множители в первой строке системы имеем:

$\begin{cases}
(x-\sqrt2)(x+\sqrt2)(x-1)(x-2)x\geq 0,
\\(x-2)(x-1)x\neq 0;
\end{cases}$

Ответ: $[-\sqrt2;0)\cup(1;\sqrt2]\cup(2;+\infty)$.