Производная функции

Елена Репина 2013-08-06 2021-06-30

Определение производной

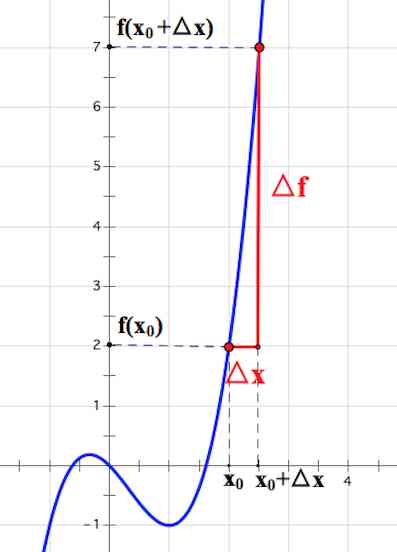
Производной функции $f(x)$ в точке $x_0$ называется предел отношения приращения функции $\Delta f=f(x_0+\Delta x)-f(x_0)$ к приращению аргумента $\Delta x$ при $\Delta x\rightarrow 0$ , если этот предел существует.

$f'(x_0)=\lim_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

Пример. + показать

Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…

Работу нам упростит таблица производных и правила дифференцирования

Геометрический смысл производной

+ показать

Поэтому геометрический смысл производной таков:

Производная в точке $x_0$ равна тангенсу угла наклона касательной к графику функции $f(x)$ в этой точке:

$f'(x_0)=tg\alpha$ ,

где $\alpha$ – угол наклона касательной (проведенной к $f(x)$ в т. $x_0$ )

Физический смысл производной

Если точка движется вдоль оси $x$ и ее координаты изменяются по закону $x(t)$ , то мгновенная скорость точки:

$v(t)=x'(t)$ ,

а ускорение:

$a(t)=v'(t)=x''(t)$

Пример. Материальная точка движется прямолинейно по закону $x(t)=6t^2-48t+17$ , где $x(t)$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени $t=9$ .