Часть 1
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
$sinx\vee a$,
$cosx\vee a$,
$tgx\vee a$,
$ctgx\vee a$,
где $\vee$ – один из знаков $<,\;>,\;\leq,\;\geq$, $a\in R$.
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
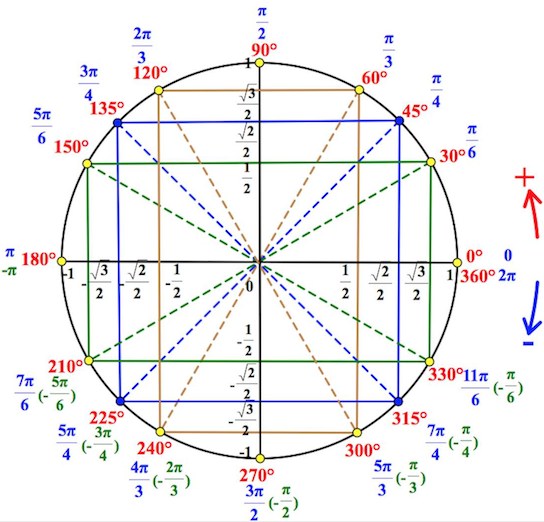
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1
Решить неравенство: $cosx<\frac{1}{2}.$
Решение: + показать
Отмечаем на оси косинусов $\frac{1}{2}.$
Все значения $cosx$, меньшие $\frac{1}{2},$ – левее точки $\frac{1}{2}$ на оси косинусов.
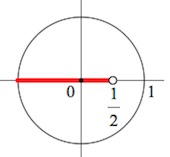
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше $\frac{1}{2}.$
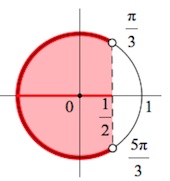
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки $\frac{\pi}{3}$ до $\frac{5\pi}{3}$.
Обратите внимание, многие, назвав первую точку $\frac{\pi}{3},$ вместо второй точки $\frac{5\pi}{3}$ указывают точку $-\frac{\pi}{3}$, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения $x:$
$\frac{\pi}{3}+2\pi n<x<\frac{5\pi}{3}+2\pi n,\;n\in Z.$
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик $2\pi n,\;n\in Z.$
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2
Решить неравенство: $cosx\geq -\frac{\sqrt2}{2}.$
Решение: + показать
Отмечаем на оси косинусов $-\frac{\sqrt2}{2}.$
Все значения $cosx$, большие или равные $-\frac{\sqrt2}{2}$ – правее точки $-\frac{\sqrt2}{2}$, включая саму точку.
Тогда выделенные красной дугой аргументы $x$ отвечают тому условию, что $cosx\geq -\frac{\sqrt2}{2}$.
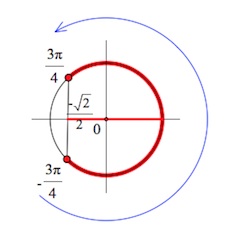$-\frac{3\pi}{4}+2\pi n\leq x\leq \frac{3\pi}{4}+2\pi n,\; n\in Z.$
Пример 3
Решить неравенство: $sinx\geq -\frac{\sqrt3}{2}.$
Решение:+ показать
Отмечаем на оси синусов $-\frac{\sqrt3}{2}.$
Все значения $sinx$, большие или равные $-\frac{\sqrt3}{2},$ – выше точки $-\frac{\sqrt3}{2}$, включая саму точку.
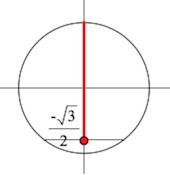
«Транслируем» выделенные точки на тригонометрический круг:
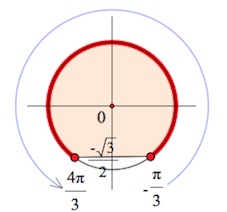$-\frac{\pi}{3}+2\pi n \leq x\leq \frac{4\pi}{3}+2\pi n,\;n\in Z$
Пример 4
Решить неравенство: $sinx<1.$
Решение:+ показать
Кратко:
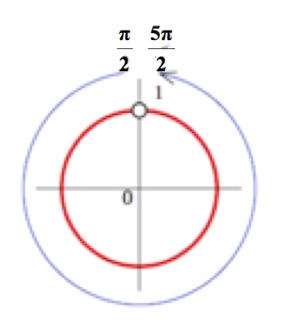
$\frac{\pi}{2}+2\pi n<x<\frac{5\pi}{2}+2\pi n,\;n\in Z$
или все $x$, кроме $\frac{\pi}{2}+2\pi n,\;n\in Z.$
Пример 5
Решить неравенство: $sinx\geq 1.$
Решение:+ показать
Неравенство $sinx\geq 1$ равносильно уравнению $sinx=1$, так как область значений функции $y=sinx$ – $[-1;1].$
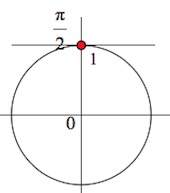
$x=\frac{\pi}{2}+2\pi n,\;n\in Z.$
Пример 6
Решить неравенство: $sinx<\frac{1}{3}.$
Решение:+ показать
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
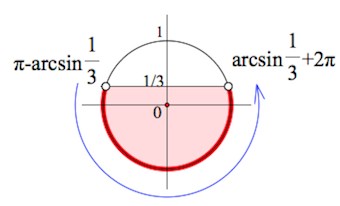
$\pi -arcsin\frac{1}{3}+2\pi n<x<arcsin\frac{1}{3}+2\pi+2\pi n,\;n\in Z$
Если не очень понятно, загляните сюда –>[spoiler]
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен $\frac{1}{3},\;-\frac{1}{3}?$
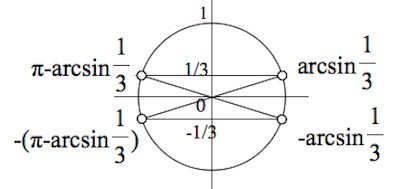
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому
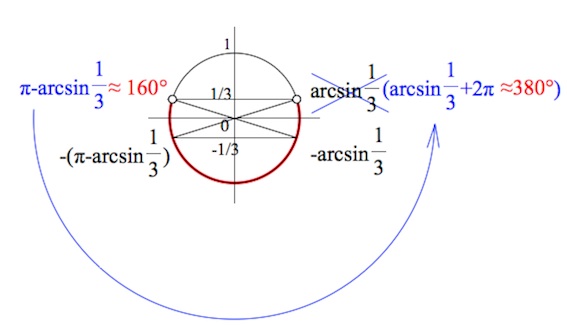
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так: $\frac{5\pi}{4}+2\pi n\leq x\leq \frac{11\pi}{4}+2\pi n,\; n\in Z.$
1. Решить неравенство: $sinx<-\frac{1}{2}.$
Ответ: + показать
$(-\frac{5\pi}{6}+2\pi n;-\frac{\pi}{6}+2\pi n),\;n\in Z$
2. Решить неравенство: $cosx>-\frac{1}{2}.$
Ответ: + показать
$(-\frac{2\pi}{3}+2\pi n;\frac{2\pi}{3}+2\pi n),\;n\in Z$
3. Решить неравенство: $sinx\geq -1.$
Ответ: + показать
$(-\infty;+\infty)$
4. Решить неравенство: $sinx\geq 0.$
Ответ: + показать
$[2\pi n;\pi +2\pi n,\;n\in Z]$
5. Решить неравенство: $cosx\leq 0,2.$
Ответ: + показать
$[arccos0,2+2\pi n;2\pi-arccos0,2+2\pi n,\;n\in Z]$
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Как можно решить такие неравенство
Sinx>0
tgx <0
cosx0
Пользуясь точно таким же алгоритмом, что использован при решении разобранных в статье неравенств…
Cgtx>0
Решила
Решите систему неравенств:
Sinx больше или равно 1/3
Cos меньше 7/8
Буду очень благодарна)
На одном тригонометрическом круге решаете графически оба неравенства. Первое – дуга, что над 1/3 (включая концы), второе – дуга, что левее 7/8. Пересекаете дуги. Один конец дуги – arccos7/8 +2pin, второй – pi-arcsin 1/3 +2pin. Делайте вывод.
Tg(П+х) меньше1 Как решить с помощью круга
Сначала примените формулы приведения!
Помогите пожалуйста)
cosX<-корень из 3/2
Марина, посмотрите решение примера №1.
помогите пожалуйста решить: 1) sin x >1/2 2) cos(x+ Pi/12)0
Второе неравенство у вас криво написано, первое аналогично примеру 3. Если разбор аналогичного задания вам не помогает, то дело плохо и вам сперва нужно подружиться с тригонометрическим кругом
не могу решить, помогите,пожалуйста 2cos^2x+cosx≤0
2cos^2x+cosx<=0 Cosx(2cosx+1)<=0 На оси косинусов отмечайте 0, -1/2. Между этими точками (включая точки) - искомые значения косинуса. Осталось понять, какие аргументы соответствуют отреку [-1/2;0]. От -2пи/3+2пиn до -пи/2+2пиn и от пи/2+2пиn до 2пи/3 +2пиn включительно, не так ли?
Помогите, пожалуйста, школу давно закончила, дочке не могу объяснить. Заранее спасибо.
Найти сумму решений, удовлетворяющих неравенству: |x+2pi/3|<=pi/2
[latexpage]$|x+\frac{2\pi}{3}|\leq \frac{\pi}{2};$
$-\frac{\pi}{2}\leq x+\frac{2\pi}{3}\leq \frac{\pi}{2};$
$-\frac{\pi}{2}-\frac{2\pi}{3}\leq x\leq \frac{\pi}{2}-\frac{2\pi}{3};$
$-\frac{7\pi}{6}\leq x\leq -\frac{\pi}{6}.$
А про сумму решений ничего не могу ответить – не понимаю вопроса…
Помогите пожалуйста)
2cos(45(градусов)-3x)>= -sqrt2
[latexpage]$2cos(45^{\circ}-3x)\geq -\sqrt2;$
$cos(45^{\circ}-3x)\geq -\frac{\sqrt2}{2};$
$-\frac{3\pi}{4}+2\pi n \geq 45^{\circ}-3x\geq \frac{3\pi}{4}+2\pi n, n\in Z;$
…
А скажите пожалуйста как находить P1 И P2 Все никак не могу понять
Простите, я не могу понять, что вы хотите…
Здравствуйте! Пожалуйста объясните ответ к заданию 5,не понятно просто,особенно часть: 2п-arccos0,2+2пn. Я не понимаю почему 2п-arccos0,2? Я вообще не очень понимаю как записываются ответы с arccos,arcsin понятен,а вот arccosin нет,помогите,пожалуйста.
Павел, скажите, что по-вашему, должно быть вместо 2пи-arccos0,2+2пиn?
И ещё вопрос: как вы считаете, arccos 0,2 – это сколько примерно (очень примерно) в градусах?
Если вы ответите, я возможно смогу понять где вы заблуждаетесь…
arccos0,2-это примерно 78°,но видимо я не корректно поставил вопрос. Я не понимаю что вообще на этом месте ставится и почему,точнее всегда ли ставится вначале 2п или это индивидуально для каждого примера
Хорошо. А когда мы проводили вертикаль к оси косинусов через 0,2, мы же тригонометрическую окружность пересекали дважды? Как по вашему можно примерно в градусах определить точку, что ниже второй? И понимаете ли вы, что указывая промежуток, мы должны следить за тем, чтобы левый конец был бы меньше правого?
Ааа,до меня дошло,спасибо вам!