Задача 1. В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $AB=12,\;cosA=0,25.$ Найдите AC.
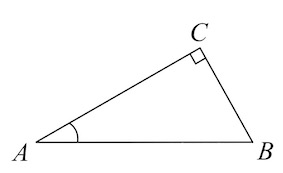
Решение: + показать
Определение косинуса угла смотрите здесь
$cosA=\frac{AC}{AB};$
$\frac{1}{4}=\frac{AC}{12};$
$AC=3.$
Ответ: $3.$
Задача 2. В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $sinA=\frac{8}{17},\;AB=17.$ Найдите $AC.$

Решение: + показать
Определение синуса угла смотрите здесь
$sinA=\frac{BC}{AB};$
$\frac{8}{17}=\frac{BC}{17};$
$BC=8.$
Тогда по т. Пифагора
$AC=\sqrt{17^2-8^2}=15.$
Ответ: $15.$
Задача 3. В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $AB=1,5,\;tgA=\frac{5}{\sqrt{20}}.$ Найдите AC.

Решение: + показать
Способ 1
Воспользуемся формулой
$1+tg^2A=\frac{1}{cos^2A};$
Так как $tgA=\frac{5}{\sqrt{20}}$, то
$1+\frac{25}{20}=\frac{1}{cos^2x};$
$\frac{45}{20}=\frac{1}{cos^2x};$
$\frac{4}{9}=cos^2x;$
Поскольку $\angle A$ – острый, то $cosA=\frac{2}{3};$
Наконец,
$cosA=\frac{AC}{AB};$
$\frac{3}{2}=\frac{AC}{1,5};$
$AC=1;$
Способ 2
Так как $tgA=\frac{5}{\sqrt{20}}=\frac{BC}{AC}$, то пусть $BC=5x,\;AC=\sqrt{20}x.$
По т. Пифагора
$1,5^2=(5x)^2+(\sqrt{20}x)^2;$
$1,5^2=45x^2;$
$x=\frac{1,5}{\sqrt{45}}.$
Тогда
$AC=\sqrt{20}x=\sqrt{20}\cdot \frac{1,5}{\sqrt{45}}=1.$
Ответ: $1.$
Задача 4. В треугольнике $ABC$ угол $C$ равен $90$°, $AC=7,BC=24.$ Найдите $SinA.$

Решение: + показать
$sinA=\frac{BC}{AB}=\frac{24}{\sqrt{AC^2+BC^2}}=\frac{24}{\sqrt{7^2+24^2}}=\frac{24}{25}=0.96.$
Ответ: $0,96.$
Задача 5. В треугольнике $ABC$ угол $C$ равен $90$°, высота $CH$ равна $1,$ $BC=\sqrt2.$ Найдите $tgA.$
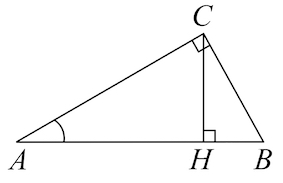
Решение: + показать
$\angle A=\angle BCH,$ поэтому
$tgA=tg BCH=\frac{BH}{CH}=\frac{\sqrt{BC^2-CH^2}}{CH}=\frac{\sqrt{(\sqrt2)^2-1}}{1}=1.$
Ответ: $1.$
Задача 6. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $BC=12,BH=3.$ Найдите $sinA.$

Решение: + показать
$sinA=sinBCH=\frac{BH}{BC}=\frac{3}{12}=0,25.$
Ответ: $0,25.$
Задача 7. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $BC=3\sqrt{65}, BH=21.$ Найдите $tgA.$

Решение: + показать
$tgA=tgBCH=\frac{BH}{CH}=\frac{21}{\sqrt{BC^2-BH^2}}=$
$=\frac{21}{\sqrt{(3\sqrt{65})^2-21^2}}=\frac{21}{12}=1,75.$
Ответ: $1,75.$
Задача 8. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $AB=10,tgA=\frac{1}{3}.$ Найдите $BH.$

Решение: + показать
Треугольник $ABC:$
$tgA=\frac{1}{3},$ тогда $BC=x,AC=3x.$
$(3x)^2+x^2=10^2;$
$10x^2=100;$
$x=\sqrt{10}.$

Треугольник $BCH:$
$tgA=tgBCH=\frac{1}{3},$ тогда $BH=y,CH=3y.$
$(3y^2)+y^2=(\sqrt{10})^2;$
$y=1.$
Ответ: $1.$
Задача 9. В треугольнике $ABC$ угол $C$ равен $90$°, $BC=25, SinA=\frac{3}{5}.$ Найдите высоту $CH.$

Решение: + показать
$\angle A=\angle BCH,$ поэтому $sin BCH=\frac{3}{5}.$
Пусть тогда $BH=3x, BC=5x.$

А так как $BC=25$ по условию, то
$5x=25;$
$x=5.$
Далее, так как $CH=4x$ (по теореме Пифагора из треугольника $BCH$), то
$CH=4\cdot 5=20.$
Ответ: $20.$
Задача 10. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $BC=8, Sin A=0,25.$ Найдите $BH.$

Решение: + показать
$\angle A=\angle BCH,$ поэтому $sin BCH=sinA=0,25=\frac{1}{4}.$
Тогда пусть в треугольнике $BCH$ $BH=x, BC=4x.$

А поскольку $BC=8,$то
$8=4x,$
откуда
$x=BH=2.$
Ответ: $2.$
Задача 11. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $BC=7,$ $cosA=\frac{\sqrt{33}}{7}.$ Найдите $AH.$

Решение: + показать
Треугольник $ABC:$
$CosA=\frac{\sqrt{33}}{7},$ тогда пусть $AC=\sqrt{33}x, AB=7x.$
Стало быть,
$(\sqrt{33}x)^2+7^2=(7x)^2;$
$16x^2=7^2;$
$x=\frac{7}{4}.$

Треугольник $ACH:$
$CosA=\frac{\sqrt{33}}{7},$ тогда пусть $AH=\sqrt{33}y, AC=7y.$
Имеем:
$AC=\sqrt{33}x=7y;$
$y=\frac{\sqrt{33}\cdot \frac{7}{4}}{7}=\frac{\sqrt{33}}{4}.$
Стало быть,
$AH=\sqrt{33}y=\sqrt{33}\cdot \frac{\sqrt{33}}{4}=\frac{1}{4}=0,25.$
Ответ: $0,25.$
Задача 12. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$ — высота, $AH=27,tgA=\frac{1}{3}.$ Найдите $BH.$

Решение: + показать
Треугольник $ACH:$
$tgA=\frac{CH}{AH},$ тогда пусть $CH=x, AH=3x.$
А так как по условию $AH=27,$ то $3x=27,$ то есть $x=9.$
 Треугольник $BCH:$
Треугольник $BCH:$
$tgA=tgBCH=\frac{BH}{CH},$ тогда пусть $BH=y,CH=3y.$
В тоже время $CH=x.$
Стало быть, $3y=9,$ $y=3.$
Ответ: $3.$
Задача 13. В треугольнике $ABC$ угол $C$ равен 90°, угол $A$ равен $30^{\circ},\;AB=2\sqrt3.$ Найдите высоту $CH$.

Решение: + показать
Из треугольника $ABC:$
$BC=\frac{AB}{2},$ так как катет $BC$ лежит против угла в $30^{\circ}.$
$BC=\frac{2\sqrt3}{2}=\sqrt3.$
Значит по т. Пифагора
$AC=\sqrt{AB^2-BC^2}=\sqrt{(2\sqrt3)^2-(\sqrt3)^2}=3.$
Из треугольника $ACH$:
$CH=\frac{AC}{2}$, так как катет $CH$ лежит напротив угла в $30^{\circ}.$
$CH=1,5.$
Ответ: $1,5.$
Задача 14. В треугольнике $ABC$ угол $C$ равен $90$°, $CH$— высота, угол $A$ равен $30^{\circ},$ $AB=60.$ Найдите $AH.$

Решение: + показать
Из треугольника $ABC:$
$BC=\frac{AB}{2}=\frac{60}{2}=30,$
так как катет $BC$ лежит против угла в $30^{\circ}.$
Аналогично из треугольника $CBH:$
$BH=\frac{BC}{2}=\frac{30}{2}=15.$
Тогда
$AH=AB-BH=60-15=45.$

Ответ: $45.$

Вы можете пройти тест по теме «Прямоугольный треугольник»





















 Треугольник $BCH:$
Треугольник $BCH:$
Добавить комментарий