Задача 1. В треугольнике $ABC$ $AC=BC=4, sin B=\frac{3\sqrt{11}}{10}.$ Найдите $AB.$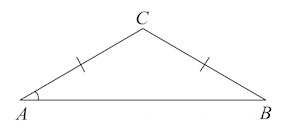
Решение: + показать
Пусть $CH\perp AB$ (заметим, $H$ – середина $AB$ по свойству равнобедренного треугольника).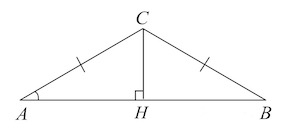
В треугольнике $ACH:$
$sinA=sinB=\frac{CH}{AC};$
$\frac{3\sqrt{11}}{10}=\frac{CH}{4};$
$CH=\frac{6\sqrt{11}}{5}.$
Тогда по теореме Пифагора (треугольник $ACH$):
$AH^2=AC^2-CH^2=4^2-(\frac{6\sqrt{11}}{5})^2=16-\frac{396}{25}=\frac{4}{25}.$
Откуда $AH=0,4$ и, наконец, $AB=0,8.$
Ответ: $0,8.$
Задача 2. В треугольнике $ABC$ $AC=BC, AB=2\sqrt{51},sinA=0,7.$ Найдите $AC.$
Решение: + показать
Пусть $CH\perp AB$ (заметим, $H$ – середина $AB$ по свойству равнобедренного треугольника).В треугольнике $ACH:$
$sinA=\frac{CH}{AC};$
$0,7=\frac{CH}{AC};$
$CH=0,7AC.$
По теореме Пифагора (треугольник $ACH$):
$AC^2=AH^2+CH^2;$
$AC^2=(\sqrt{51})^2+(0,7AC)^2;$
$0,51AC^2=51;$
$AC=10.$
Ответ: $10.$
Задача 3. В треугольнике $ABC$ $AC=BC=1,5, tgA=\frac{5}{\sqrt{20}}.$ Найдите $AB.$
Решение: + показать
Пусть $CH\perp AB$ (заметим, $H$ – середина $AB$ по свойству равнобедренного треугольника).В треугольнике $ACH:$
$tgA=\frac{CH}{AH};$
$\frac{5}{\sqrt{20}}=\frac{CH}{AH};$
$CH=\frac{5AH}{\sqrt{20}}.$
По теореме Пифагора (треугольник $ACH$):
$AC^2=AH^2+CH^2;$
$\frac{9}{4}=AH^2+(\frac{5AH}{\sqrt{20}})^2;$
$\frac{9}{4}=AH^2+\frac{25AH^2}{20};$
$\frac{9}{4}=\frac{45AH^2}{20};$
$AH=1.$
Откуда $AB=2.$
Ответ: $2.$
Задача 4. В треугольнике $ABC$ $AC=BC, AB=20, sinBAC=0,8.$ Найдите высоту $AH.$
Решение: + показать
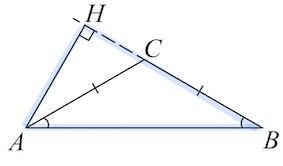
$sin BAC=sin B=\frac{AH}{AB};$
$0,8=\frac{AH}{20};$
$AH=16.$
Задача 5. В тупоугольном треугольнике $ABC$ $AC=BC=4,$ высота $AH$ равна $2.$ Найдите $sinACB.$
Решение: + показать
Треугольник $ACH:$
$sin ACH=\frac{AH}{AC}=\frac{2}{4}=0,5.$
Далее, учитывая формулу приведения $sin(180^{\circ}-\alpha)=sin\alpha,$ имеем:
$sinACB=sin(180^{\circ}-\angle ACH)=sin ACH=0,5.$
Ответ: $0,5.$
Задача 6. В тупоугольном треугольнике $ABC$ $AC=BC=25,$ высота $AH$ равна $7.$ Найдите косинус угла $ACB$.
Решение: + показать
Треугольник $ACH:$
$cos ACH=\frac{CH}{AC}=\frac{\sqrt{AC^2-AH^2}}{AC}=\frac{\sqrt{25^2-7^2}}{25}=\frac{24}{25}=0,96.$
Далее, учитывая формулу приведения $cos(180^{\circ}-\alpha)=-cos\alpha,$ имеем:
$cosACB=cos(180^{\circ}-\angle ACH)=-cos ACH=-0,96.$
Ответ: $-0,96.$
Задача 7. В тупоугольном треугольнике $ABC$ $AC=BC=\sqrt{181},$ высота $AH$ равна $9.$ Найдите $tgACB.$
Решение: + показать
Треугольник $ACH:$
$tg ACH=\frac{AH}{CH}=\frac{AH}{\sqrt{AC^2-AH^2}}=\frac{9}{(\sqrt{181})^2-9^2}=\frac{9}{10}=0,9.$
Далее, учитывая формулу приведения $tg(180^{\circ}-\alpha)=-tg\alpha,$ имеем:
$tgACB=tg(180^{\circ}-\angle ACH)=-tgACH=-0,9.$
Ответ: $-0,9.$
Задача 8. В треугольнике $ABC$ $AC=BC,AB=7,8, tg BAC=\frac{5}{12}.$ Найдите высоту $AH$.
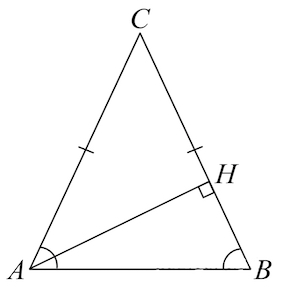
Решение: + показать
$\angle BAC=\angle ABC.$
Треугольник $ABH:$
$tgABC=\frac{AH}{HB};$
$\frac{5}{12}=\frac{AH}{HB};$
$BH=\frac{12AH}{5}.$
По теореме Пифагора:
$AB^2=AH^2+BH^2;$
$7,8^2=AH^2+(\frac{12AH}{5})^2;$
$(\frac{39}{5})^2=\frac{169AH^2}{25};$
$AH=\frac{39\cdot 5}{5\cdot 13};$
$AH=3.$
Ответ: $3.$
Задача 9. В равнобедренном треугольнике $ABC$ с основанием $AB$ боковая сторона равна $16\sqrt{15}, sinBAC=0,25.$ Найдите длину высоты $AH.$
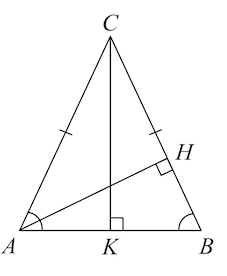
Решение: + показать
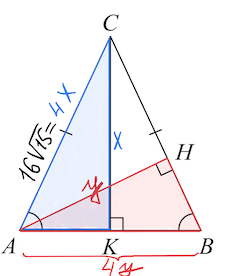
$\angle BAC=\angle ABC.$
Треугольник $ACK:$
Так как $sin BAC=\frac{CK}{AC}=\frac{1}{4},$ то пусть $CK=x,AC=4x.$
А поскольку $AC=16\sqrt{15}$ по условию, то $16\sqrt{15}=4x,$ $x=4\sqrt{15}.$
По теореме Пифагора $AK=\sqrt{AC^2-CK^2}=\sqrt{(4x)^2-x^2}=x\sqrt{15}=60.$ Откуда $AB=120.$
Треугольник $ABH:$
Так как $sin ABC=\frac{AH}{AB}=\frac{1}{4},$ то пусть $AH=y,AB=4y.$
А поскольку $AB=120,$ то $4y=120,$ $y=30.$
Итак, $AH=y=30.$
Ответ: $30.$
Задача 10. В равнобедренном треугольнике $ABC$ с основанием $AB$ боковая сторона равна $36, cos BAC=\frac{5}{6}.$ Найдите $BH.$
Решение: + показать
$\angle BAC=\angle ABC.$
Треугольник $ACK:$
Так как $cos BAC=\frac{AK}{AC}=\frac{5}{6},$ то пусть $AK=5x,AC=6x.$
А поскольку $AC=36,$ то
$36=6x;$
$x=6.$
Откуда $AK=5\cdot 6=30, AB=60.$
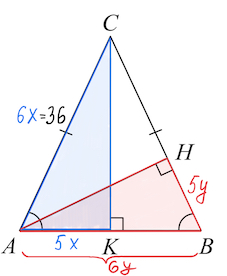
Треугольник $ABH:$
Так как $cos ABH=\frac{BH}{AB}=\frac{5}{6},$ то пусть $BH=5y,AB=6y.$
Далее
$AB=60=6y,$ откуда $y=10.$
Тогда $BH=5y=5\cdot 10=50.$
Ответ: $50.$
Задача 11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^{\circ}.$ Боковая сторона треугольника равна $14.$ Найдите площадь этого треугольника.
Решение: + показать
$S=\frac{AC\cdot BC\cdot sinC}{2}=\frac{14^2\cdot sin 30^{\circ}}{2}=\frac{14^2\cdot \frac{1}{2}}{2}=49.$
Ответ: $49.$
Задача 12. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^{\circ}.$ Найдите боковую сторону треугольника, если его площадь равна $2116.$
Решение: + показать
$S=\frac{AC\cdot BC\cdot sin30^{\circ}}{2};$
$2116=\frac{AC^2\cdot \frac{1}{2}}{2};$
$AC^2=2116\cdot 4;$
$AC=92.$
Ответ: $92.$
Задача 13. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^{\circ}.$ Боковая сторона треугольника равна $11.$ Найдите площадь этого треугольника.
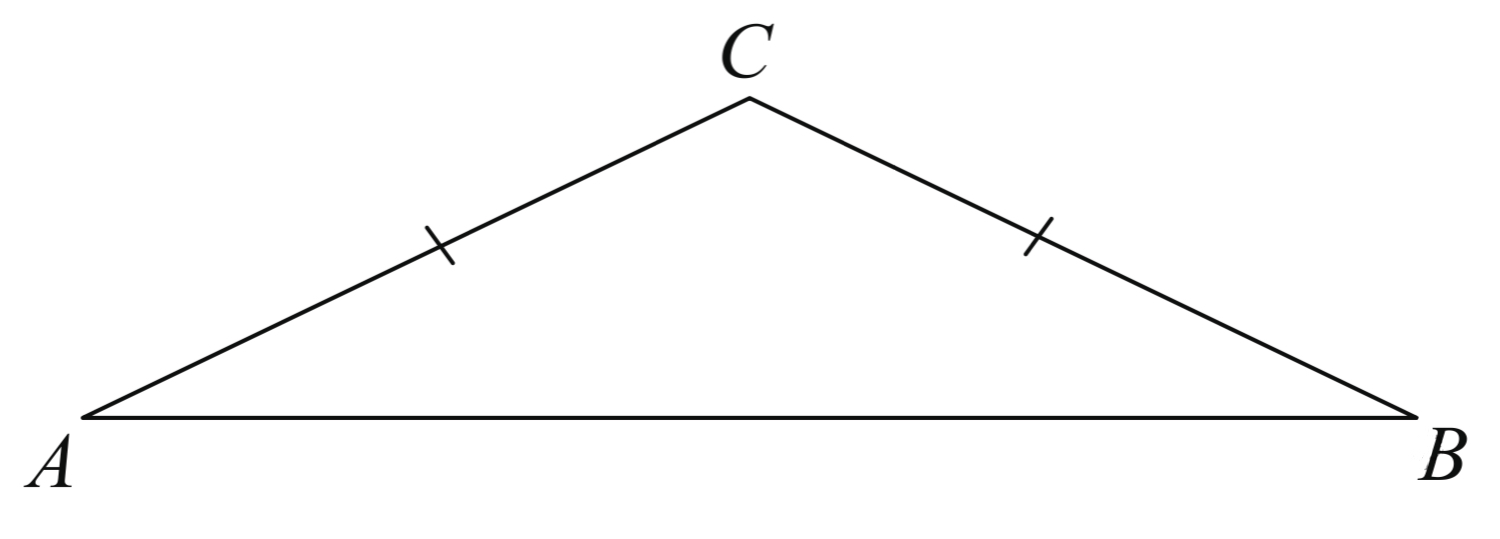
Решение: + показать
$S=\frac{AC\cdot BC\cdot sinC}{2}=\frac{11^2\cdot sin 150^{\circ}}{2}=\frac{11^2\cdot \frac{1}{2}}{2}=30,25.$
Ответ: $30,25.$
Задача 14. Боковая сторона равнобедренного треугольника равна $117,$ а основание равно $216.$ Найдите площадь этого треугольника.
Решение: + показать
Пусть $CH\perp AB.$
По свойству равнобедренного треугольника $AH=BH.$
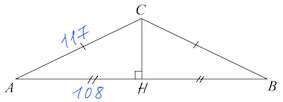
$CH=\sqrt{AC^2-AH^2}=\sqrt{117^2-108^2}=\sqrt{(117-108)(117+108)}=\sqrt{9\cdot 225}=45.$
Тогда
$S=\frac{AB\cdot CH}{2}=\frac{216\cdot 45}{2}=4860.$
Задача 15. В треугольнике $ABC$ $AB=BC=AC=8\sqrt3.$ Найдите высоту $CH.$
Решение: + показать
В равностороннем треугольнике высота $CH$ является и медианой: $AH=BH.$
$CH=\sqrt{AC^2-AH^2}=\sqrt{(8\sqrt3)^2-(4\sqrt3)^2}=12.$
Ответ: $12.$
Задача 16. В равностороннем треугольнике $ABC$ высота $CH$ равна $15\sqrt3.$ Найдите стороны этого треугольника.
Решение: + показать
В равностороннем треугольнике высота $CH$ является и медианой: $AH=BH.$
Пусть $AH=x,$ тогда $AC=2x.$
$CH^2=AC^2-AH^2;$
$(15\sqrt3)^2=(2x)^2-x^2;$
$15^2\cdot 3=3x^2;$
$x=15.$
Тогда сторона треугольника равна $30.$
Ответ: $30.$
Задача 17. В треугольнике $ABC$ $AC=BC=42,$ угол $C$ равен $30^{\circ}.$ Найдите высоту $AH$.
Решение: + показать
В прямоугольном треугольнике $ACH$ угол $C$ равен $30^{\circ},$ тогда $AC=2AH,$ откуда $AH=12.$
Ответ: $12.$
Задача 18. В треугольнике $ABC$ $AC=BC=76,$ высота $AH$ равна $38.$ Найдите угол $C.$ Ответ дайте в градусах.
Решение: + показать
В прямоугольном треугольнике $ACH$ $AC=2AH,$ значит $\angle C=30^{\circ}.$
Ответ: $30.$
Задача 19. В треугольнике $ABC$ угол $C$ равен $8^{\circ},$ $AC=BC.$ Найдите угол $A.$ Ответ дайте в градусах.
Решение: + показать
В равнобедренном треугольнике $ABC$ $\angle A=\angle B.$
Поэтому
$\angle A=(180^{\circ}-8^{\circ}):2=86^{\circ}.$
Ответ: $86.$
Задача 20. Один угол равнобедренного треугольника на $96^{\circ}$ больше другого. Найдите меньший угол. Ответ дайте в градусах.
Решение: + показать
Пусть $\angle A=\angle B=x,$ тогда $\angle C=x+96^{\circ}.$
Тогда
$x+x+(x+96^{\circ})=180^{\circ};$
$3x=84^{\circ};$
$x=28^{\circ}.$
Ответ: $28.$
Задача 21. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $120^{\circ}.$ Боковая сторона треугольника равна $2\sqrt3.$ Найдите длину основания этого треугольника.
Решение: + показать
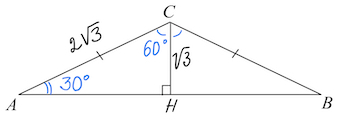
Пусть $CH\perp AB.$
Тогда в прямоугольном треугольнике $ACH$ $\angle A=30^{\circ}.$
Стало быть,
$CH=\frac{AC}{2}=\frac{2\sqrt3}{2}=\sqrt3.$
По теореме Пифагора
$AH=\sqrt{AC^2-CH^2}=\sqrt{(2\sqrt3)^2-(\sqrt3)^2}=3.$
Откуда
$AB=6.$
Ответ: $6.$
Задача 22. В треугольнике $ABC$ $AC=BC.$ Внешний угол при вершине $B$ равен $98^{\circ}.$ Найдите угол $C.$ Ответ дайте в градусах.
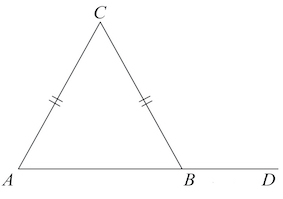
Решение: + показать
В равнобедренном треугольнике $ABC$ $\angle A=\angle B.$
Если $\angle CBD=98^{\circ},$ то $\angle ABC=180^{\circ}-98^{\circ}=82^{\circ}.$
Тогда $\angle C=180^{\circ}-\angle A-\angle B=180^{\circ}-2\cdot 82^{\circ}=16^{\circ}.$
Ответ: $16.$
Вы можете пройти тест по теме «Равнобедренный треугольник. Вычисление углов и длин».
Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
В 4-й задаче сразу несколько ошибок…
Анатолий, спасибо за замечание. Ошибка была в самом условии, потому казалось, что решение неверное. Переправила условие. Сейчас все ок ;)
Не совсем понятно решение 5-й задачи…
Анатолий, с какого момента непонятно? Спрашивайте.
Смысл в том, что мы немного переформулировали условие задачи, “подменив” условие [latexpage]$sinBAC=\frac{\sqrt3}{2}$ другим: $cosBAH=\frac{\sqrt3}{2}$
5-я задача, не понимаю из какой теоремы вы взяли что SinA=AH/AB
Раз углы CAB и CBA равны, мы утверждаем, что [latexpage] $sinB=sinA}$. При этом из треугольника ABH $sinB=\frac{AH}{AB}$
Спасибо огромное! пол дня голову над этой задачей ломал, выручили очень ;)
Мне понравилась ваша методика последовательного изучения темы, сначала прямоугольный треугольник, затем равнобедренный…
И ещё такой вопрос, когда я прохожу тесты, в конце выводится сообщение “средний результат:50% ваш результат: 75%”, так вот каким образом подсчитывается средний результат?
Анатолий, средний результат означает, что в среднем, прошедшие тест товарищи, выполняют верно только половину заданий (ну или, например, кто-то выполнил все верно, а кто-то только 2-3 задания из всех… )… Ваш результат выше!
P.S. И вам спасибо за обнаруженные опечатки! ;)
Опечатка
Задача 10.
В треугольнике ABC\;AC=BC, угол C равен 120^{\circ}, AB=2\sqrt3. Найдите AB.
Должно быть
Задача 10.
В треугольнике ABC\;AC=BC=2\sqrt3, угол C равен 120^{\circ}. Найдите AB.
Спасибо!
Задача 10 ответ 2 ( проверенно учителем)
cos A = (ah/ac)
sqt3/2=sqt3/ac
sqt3 ac = 2 sqt 3
ac = 2
Михаил, у себя ошибки не нахожу. А у вас – да.
Мы ищем не AC, а AB..
AC нам известно…