Разбор задания из пробного экзамена в МГУ в 2013 году. Система неравенств.

Предлагаю разобрать  задание  (№1) из пробного экзамена в МГУ.
Задание, так скажем, без особых премудростей. Полезно для подготовки к части С ЕГЭ по математике.
Также смотрите остальные задания этого экзамена здесь: №2, №3, №4, №5, №6, №7, №8

Условие: 

Найдите все значения $x$, удовлетворяющие одновременно двум условиям
$\begin{cases}
|x-3|+|x-4|\leq 3, &
&5x^2-31x+42\geq 0;
\end{cases}$

Решение: 

Начнем с решения второго неравенства системы: $5x^2-31x+42\geq 0.$

Будем раскладывать  квадратный трехчлен на множители

($ax^2+bx+c=a(x-x_1)(x-x_2)$, где $x_1,\;x_2$ – корни квадратного трехчлена  $ax^2+bx+c$), чтобы потом применить метод интервалов к неравенству:

Заготавливаем шаблончик $5x^2-31x+42=5(x-…)(x-…)$ и находим корни:

$5x^2-31x+42=0$ <=> $x=\frac{31\pm \sqrt{31^2-4\cdot 5\cdot 42}}{2\cdot 5}$ <=>

<=> $x_1=4,2,\;x_2=2$

Итак, $5x^2-31x+42\geq 0$ <=> $5(x-4,2)(x-2)\geq 0$

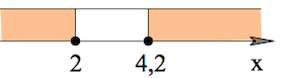
$x\in(-\infty;2]\cup[4,2;+\infty)$

Теперь решим первое неравенство системы $|x-3|+|x-4|\leq 3.$ Если вы не сталкивались еще с такими неравенствами, то советую для начала посмотреть видеоурок, в котором подробно рассматривается решение подобных неравенств.

Итак, поскольку нули модулей – точки 3 и 4, то у нас образовалось три промежутка $(-\infty;3),\;(3;4),\;(4;+\infty)$. В зависимости от того, в каком промежутке мы находимся, подмодульные выражения имеют разные знаки и распределяются они так:

1) На промежутке $x<3$ имеем:

$-x+3-x+4\leq 3$ <=> $x\geq 2$

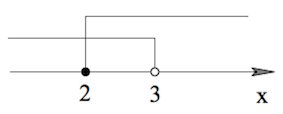
$x\in[2;3).$

2) На промежутке $3\leq x\leq 4$ имеем:

$x-3-x+4\leq 3$ <=> $1\leq 3$ – верно при всех $x$, а поскольку мы работаем на отрезке $[3;4]$, то $x\in [3;4].$

3) На промежутке $x>4$ имеем:

$x-3+x-4\leq 3$ <=> $x\leq 5$

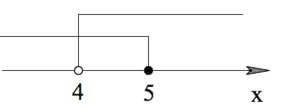
$x\in (4;5]$.

Итак, объединяя решения на трех промежутках, получаем:

$x\in[2;5]$

Все,  – нам осталось пересечь решения двух неравенств системы:

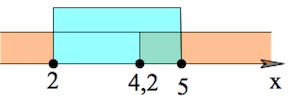
Ответ: {$2$}$\cup[4,2;5].$