Задания резервного дня сдачи ЕГЭ по математике от 28 июня 2016

a)

$sin2x+2cos(x-\frac{\pi}{2})=\sqrt3cosx+\sqrt3;$

$sin2x+2sinx=\sqrt3cosx+\sqrt3;$

$2sinxcosx+2sinx=\sqrt3cosx+\sqrt3;$

$2sinx(cosx+1)=\sqrt3(cosx+1);$

$(cosx+1)(2sinx-\sqrt3)=0;$

$cosx=-1$ или $sinx=\frac{\sqrt3}{2};$

$x=\pi +2\pi n,n\in Z$ или  $x=\frac{\pi}{3}+2\pi k$ или $x=\frac{2\pi}{3}+2\pi k, k\in Z.$

б) Произведем отбор корней  уравнения, из отрезка $[-3\pi;-\frac{3\pi}{2}]$ при помощи тригонометрического круга:

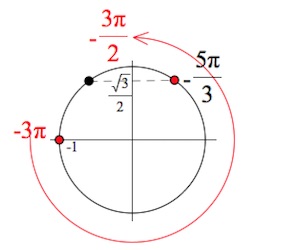
Ответ:

а) $\pi +2\pi n,n\in Z$, $\frac{\pi}{3}+2\pi k,$  $\frac{2\pi}{3}+2\pi k, k\in Z.$

б) $-3\pi;-\frac{5\pi}{3}.$ 

а) Пусть прямая $AP$ плоскости $ABC$ пересекается с прямой $BC$ в точке $T.$

Прямая $QT$ плоскости $BB_1C_1C$ пересекает прямую $CC_1$ в точке $M.$

Докажем, что $MC=MC_1.$

Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то, в частности,  $AQ\parallel PM$.

Треугольники $AQB,PMC$ подобны по двум углам. Тогда $\frac{PC}{AB}=\frac{MC}{QB},$ а значит, $\frac{8}{12}=\frac{MC}{9},$ то есть $MC=6.$

Итак, $MC=\frac{CC_1}{2},$ то есть точка $M$ является серединой ребра $CC_1.$ Что и требовалось доказать.

б) Пусть $CH\perp AT.$ По теореме о трех перпендикулярах и $MH\perp AT.$ Тогда $AT\perp (HMC)$ по признаку перпендикулярности прямой и плоскости.

Плоскости $APQ, HMC$ перпендикулярны по признаку перпендикулярности плоскостей (в плоскости $APQ$ нашлась прямая ($AT$), перпендикулярная $(HMC)$).

Перпендикулярные плоскости $APQ, HMC$ пересекаются по прямой $HM.$ По свойству перпендикулярных плоскостей, если мы проведем перпендикуляр $CE$ в плоскости $HMC$ к $HM,$ то этот перпендикуляр будет и перпендикуляром к плоскости $APQ,$ а значит расстояние от $C$ до $(APQ)$ и есть  длина $CE.$

Заметим, треугольники $APD,CPH$ подобны по двум углам, а значит,

$\frac{AP}{CP}=\frac{AD}{CH};$

$CH=\frac{CP\cdot AD}{AP}=\frac{8\cdot 12}{4\sqrt{10}}=\frac{24}{\sqrt{10}}.$

Тогда (расписав дважды площадь треугольника $MCH$), получим

$CE=\frac{CH\cdot CM}{MH}=\frac{\frac{24}{\sqrt{10}}\cdot 6}{\sqrt{6^2+(\frac{24}{\sqrt{10}})^2}}=\frac{\frac{24\cdot 6}{\sqrt{10}}}{\frac{6\sqrt{26}}{\sqrt{10}}}=\frac{24}{\sqrt{26}}=\frac{12\sqrt{26}}{13}.$

Ответ: б) $\frac{12\sqrt{26}}{13}$.

$\frac{9^x-3^{x+1}-19}{3^x-6}+\frac{9^{x+1}-3^{x+4}+2}{3^x-9}\leq 10\cdot 3^x+3;$

$\frac{9^x-3\cdot 3^{x}-19}{3^x-6}+\frac{9\cdot 9^{x}-81\cdot 3^{x}+2}{3^x-9}\leq 10\cdot 3^x+3;$

Готовимся к выделению целых частей дробей:

$\frac{(3^x-6)(3^x+3)-1}{3^x-6}+\frac{9\cdot 3^x\cdot (3^x-9)+2}{3^x-9}\leq 10\cdot 3^x+3;$

$3^x+3-\frac{1}{3^x-6}+9\cdot 3^x+\frac{2}{3^x-9}\leq 10\cdot 3^x+3;$

$\frac{2}{3^x-9}-\frac{1}{3^x-6}\leq 0;$

$\frac{3^x-3}{(3^x-9)(3^x-6)}\leq 0;$

Применяем метод рационализации:

$\frac{3^x-3^1}{(3^x-3^2)(3^x-3^{log_36})}\leq 0;$

$\frac{x-1}{(x-2)(x-log_36)}\leq 0;$

$x\in (-\infty;1]\cup (log_36;2).$

Ответ: $(-\infty;1]\cup (log_36;2).$ 

а) Поскольку медиана, проведенная к гипотенузе, равна ее половине, то  $CN=NH=NB$ и $CM=MH=MA.$ В частности, $\angle NCH=\angle NHC$ и $\angle MCH=\angle MHC.$

Углы $BCH,HCA$ в сумме дают $90^{\circ},$ а значит, и равные им соответственно углы $NHC,MHC$ в сумме дают $90^{\circ}.$

А значит, прямые $MH$ и $NH$ перпендикулярны. Что и требовалось доказать.

б) Из подобия треугольников $BCH,BAC$ имеем:

$\frac{BC}{BA}=\frac{BH}{BC},$ откуда $BC^2=12$ или $BC=2\sqrt3.$

По теореме Пифагора из  треугольника $ABC$:

$AC=\sqrt{36-12}=2\sqrt6.$

По теореме Пифагора из  треугольника $BCH$:

$CH=\sqrt{12-4}=2\sqrt2.$

Из треугольника $MCH$ по теореме Косинусов:

$CH^2=2CM^2-2CM^2\cdot cos\alpha,$ где $\alpha =\angle CMH;$

$cos\alpha =\frac{2\cdot 6-8}{2\cdot 6}=\frac{1}{3};$

$sin\alpha=\sqrt{1-(\frac{1}{3})^2}=\frac{2\sqrt2}{3}.$

Тогда  из треугольника $CMQ$

$QM=\frac{\sqrt6}{cos\alpha}=3\sqrt6.$

Треугольники $PNC,QNH$ равны по катету и острому углу.

Имеем: $PM=QM.$

Итак, $S_{PQM}=\frac{1}{2}\cdot PM^2\cdot sin \alpha =\frac{1}{2}\cdot 9\cdot 6\cdot \frac{2\sqrt2}{3}=18\sqrt2.$

Ответ: б) $18\sqrt2.$ 

На счету вкладчика спустя год после открытия вклада:

$10\cdot 1,1$ млн. рублей.

На счету вкладчика спустя два года после открытия вклада:

$10\cdot 1,1^2$ млн. рублей.

На счету вкладчика на начало третьего года после открытия вклада:

$10\cdot 1,1^2+x$ млн. рублей.

На счету вкладчика спустя три года после открытия вклада:

$10\cdot 1,1^3+1,1\cdot x$ млн. рублей.

На счету вкладчика на начало четвертого года после открытия вклада:

$10\cdot 1,1^3+1,1\cdot x+x$ млн. рублей.

На счету вкладчика спустя четыре года после открытия вклада:

$10\cdot 1,1^4+1,1^2\cdot x+1,1\cdot x$ млн. рублей.

Итак, прирост денежных средств составит:

$10\cdot 1,1^4+1,1^2\cdot x+1,1\cdot x-(10+2x)$ млн. рублей.

А поскольку банк за четыре года начислит на вклад больше $7$ млн. рублей, то составим и решим неравенство:

$10\cdot 1,1^4+1,1^2\cdot x+1,1\cdot x-(10+2x)>7;$

$x(1,1^2+1,1-2)>17-10\cdot 1,1^4;$

$x>\frac{2,359}{0,31};$

$x>\frac{2359}{310};$

$x>7\frac{189}{310};$

Нас интересует наименьшее целое значение $x$, удовлетворяющее неравенству. Это $8.$

Ответ: $8.$ 

$\begin{cases}(x-3)(y+3x-9)=|x-3|^3,\\y=x+a;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}\begin{cases}x\geq 3,\\(x-3)(y+3x-9)-(x-3)^3=0;\end{cases}\\\begin{cases}x<3,\\(x-3)(y+3x-9)+(x-3)^3=0;\end{cases}\end{array}\right.\\y=x+a;&\end{cases}$

$\begin{cases}\left[\begin{array}{rcl}\begin{cases}x\geq 3,\\(x-3)((y+3x-9)-(x-3)^2)=0;\end{cases}\\\begin{cases}x<3,\\(x-3)(y+3x-9)+(x-3)^2)=0;\end{cases}\end{array}\right.\\y=x+a;&\end{cases}$

В первой строке исходной системы в итоге наблюдаем:

если  $x\geq 3,$  то  $x=3$  или  $y=x^2-9x+18;$

если  $x<3,$  то  $y=-x^2+3x.$

Первая строка исходной системы уравнений задает объединение прямой $x=3,$ частей парабол$y=x^2-9x+18,x>3$,  $y=3x-x^2,x<3.$

Вторая строка системы – семейство параллельных прямых, идущих под углом $45^{\circ}$ к положительному направлению оси $(ox).$

На рисунке зеленым цветом выделена зона, в которой могут располагаться прямые $y=x+a$, чтобы исходная система имела бы $4$ решения. Границы зоны (открытые) – прямые, касающиеся указанных выше частей парабол. Также «прокалываем» зону прямой $y=x-3$ (при $a=-3$ имеем три решения; $a$ найдено из условия прохождения прямой $y=x+a$ через точку $(3;0)$).

Значение $a$, отвечающее за касание прямой $y=x+a$ и части параболы $y=-x^2+3x,x<3$ находим из условия $D=0$ для $x+a=-x^2+3x:$

$a=1.$

Значение $a$, отвечающее за касание прямой $y=x+a$ и части параболы $y=x^2-9x+18,x>3$ находим из условия $D=0$ для $x+a=x^2-9x+18:$

$25-18+a=0;$

$a=-7.$

Итак, исходная система имеет четыре решения при $a\in (-7;-3)\cup (-3;1).$

Ответ: $(-7;-3)\cup (-3;1).$ 

а) Cреднее арифметическое всех чисел – это $4$, так как $\frac{5\cdot 10+4\cdot 10+3\cdot 10}{30}=4$.

Пусть в первую группу входят  все десять пятерок, во вторую – оставшиеся числа. Тогда среднее арифметическое $A$ чисел первой группы – $5,$ среднее арифметическое $B$ чисел второй группы – $\frac{4\cdot 10+3\cdot 10}{20}=3,5.$

Тогда $\frac{A+B}{2}=\frac{17}{4}=4\frac{1}{4}.$

Итак, среднее арифметическое всех чисел меньше $\frac{A+B}{2}$.

б) Пусть сумма 15-ти чисел, попавших в первую группу, – $S_1,$ сумма чисел, попавших во вторую группу, – $S_2.$ При этом $S_1+S_2=120.$

Тогда

$A=\frac{S_1}{15}, $ $B=\frac{S_2}{15}.$

$\frac{A+B}{2}={\frac{\frac{S_1}{15}+\frac{S_2}{15}}}{2}=\frac{S_1+S_2}{30}=\frac{120}{30}=4.$

в) Если разделить числа на две равные по количеству чисел группы, то $\frac{A+B}{2}=4$ (из пункта (б)). Однако мы видели (пункт (а)), что $\frac{A+B}{2}$ может быть больше $4$.

Пусть для определенности количество чисел первой группы меньше количества чисел второй группы.

Пусть в первую группу попало $n$ чисел, тогда во вторую – $30-n$ ($n\in [1;14]$).

Согласно условию $nA+(30-n)B=120$.

$B=\frac{120-nA}{30-n}.$

Далее,

$\frac{A+B}{2}=\frac{A+\frac{120-nA}{30-n}}{2}=\frac{30A-nA+120-nA}{2(30-n)}=\frac{A(15-n)+60}{30-n}.$

Заметим, $A(15-n)>0.$

Очевидно, $A\leq 5.$ Тогда

$\frac{A+B}{2}\leq \frac{5(15-n)+60}{30-n}=\frac{135-5n}{30-n}=\frac{5(30-n)-15}{30-n}=5-\frac{15}{30-n}.$

 Далее,

$5-\frac{15}{30-n}\leq 5-\frac{15}{30-1}=5-\frac{15}{29}=4\frac{14}{29}.$

Итак, $\frac{A+B}{2}\leq 4\frac{14}{29},$ причем $\frac{A+B}{2}=4\frac{14}{29}$, когда $n=1,A=5.$

Наибольшее значение $\frac{A+B}{2}$ принимает в случае, когда в первую группу попадает одна пятерка, во вторую – все остальные исходные числа.

Ответ: 

а) все пятерки в одной группе, остальные числа – в другой;

в) $4\frac{14}{29}.$