С2 (№14). Досрочный ЕГЭ по математике от 31 марта 2017

Смотрите также 1-12; №13; №15; №16; №17; №18; №19 профильного Досрочного ЕГЭ по математике от 31.03.17

14. Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$, содержащей прямую $BD_1$ и параллельной прямой $AC,$ является ромб.

а) Докажите, что грань $ABCD$ – квадрат.

б) Найдите угол между плоскостями $\alpha$ и $BCC_1,$ если $AA_1=6,$ $AB=4.$ 

Решение:

а) Пусть плоскости $ACC_1, BDD_1$ пересекаются по прямой $KK_1,$ где $K,K_1$ – центры оснований $ABC,A_1B_1C_1$ параллелепипеда. Прямая $BD_1$ пересечет плоскость $ACC_1$ в точке на прямой $KK_1,$ назовем ее $N.$ По свойству прямой, параллельной плоскости, плоскость $ACC_1,$ содержащая $AC$, пересечет  (а общая точка есть – $N$) плоскость $\alpha$ по прямой, параллельной $AC.$

Строим в плоскости  $ACC_1$ через $N$ прямую $TF,$ параллельную $AC$ (точки $T,F$ принадлежат соответственно ребрам $AA_1,CC_1$).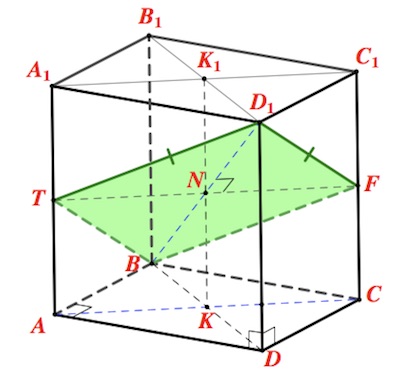

Итак, $BTD_1F$ – сечение заданного параллелепипеда плоскостью $\alpha.$

Поскольку по условию сечение – ромб, то $TF\perp BD_1$ по свойству диагоналей ромба. Но тогда и $AC\perp BD_1.$

По теореме от трех перпендикулярах, раз наклонная $BD_1$ к плоскости $ABC$ перпендикулярна $AC$, то и ее проекция $BD$ на плоскость $ABC$ перпендикулярна $AC.$ То есть в прямоугольнике $ABCD$ диагонали перпендикулярны, а значит, этот прямоугольник $ABCD$ – квадрат.

Что и требовалось доказать.

б) Построим в плоскости $BCC_1$ перпендикуляр $C_1P$ к $BF,$ линии пересечения плоскостей $\alpha$ и $BCC_1$.

По теореме о трех перпендикулярах наклонная $D_1P$ к плоскости $BCC_1$ перпендикулярна $BF$, раз ее проекция $C_1P$ на плоскость $BCC_1$ перпендикулярна $BF.$

Итак, $\angle D_1PC_1$ – угол между плоскостями $\alpha$ и $BCC_1$.

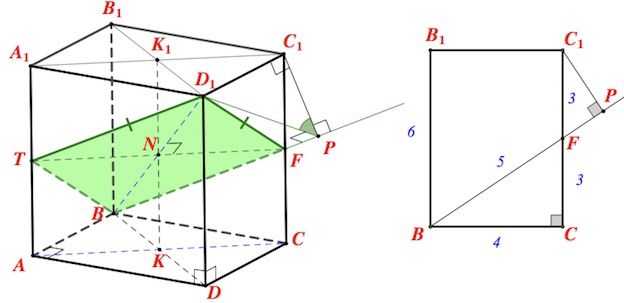
Замечая равенство $CF,FC_1$ и подобие треугольников $C_1PF,BCF,$ получаем

$C_1P:BC=C_1F:BF;$

$C_1P:4=3:5;$

$C_1P=\frac{12}{5}.$

Наконец, из треугольника $D_1C_1P$

$tg \angle D_1PC_1=\frac{D_1C_1}{C_1P}=\frac{4}{\frac{12}{5}}=\frac{5}{3}.$

То есть искомый угол – это $arctg \frac{5}{3}.$

Ответ: б) $arctg \frac{5}{3}.$