Главная › 14 (С3) Неравенства › С3 диагностической работы от 12 декабря 2013 года

13 Дек 2013

Категория: 14 (С3) НеравенстваРациональные выражения, уравнения и неравенства

С3 диагностической работы от 12 декабря 2013 года

Елена Репина 2013-12-13 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Рассмотрим С3 Д/Р без логарифмов.
Здесь можно посмотреть С3 диагностической работы без производной.

Решите систему неравенств:

$\begin{cases} 1-\frac{2}{|x|}\leq \frac{23}{x^2},\;(1)& & \frac{2-(x-5)^{-1}}{2(x-5)^{-1}-1}\leq -0,5;\;(2) \end{cases}$

Решение:

Решаем (1) неравенство системы:

Поскольку $x^2=|x|^2$ , то перед нами неравенсвто относительно переменной $|x|$ :

$1-\frac{2}{|x|}\leq \frac{23}{|x|^2};$

Домножаем обе части неравенства на $|x|^2$ , понимая, что $x\neq 0$ :

$|x|^2-2|x|-23\leq 0,\;x\neq 0;$

Раскладываем квадратный трехчлен $|x|^2-2|x|-23$ на множители (через дискриминант):

$(|x|-(1+2\sqrt 6))(|x|-(1-2\sqrt6))\leq 0,\;x\neq 0;$

Заметим, $|x|+2\sqrt 6-1>0$ , так как $2\sqrt 6-1>0.$ Поэтому мы можем переписать неравенство так:

$|x|-(1+2\sqrt 6)\leq 0,\;x\neq 0;$

$|x|\leq 1+2\sqrt 6, \;x\neq 0;$

$-1-2\sqrt 6\leq x\leq 1+2\sqrt 6,\;x\neq 0;$

Решаем (2) неравенство системы:

Мы замечаем неравенство относительно переменной $(x-5)^{-1}$ :

$\frac{2-(x-5)^{-1}}{2(x-5)^{-1}-1}+0,5\leq 0;$

Приводим к общему знаменателю:

$\frac{2-(x-5)^{-1}+0,5(2(x-5)^{-1}-1)}{2(x-5)^{-1}-1}\leq 0;$

$\frac{2-(x-5)^{-1}+(x-5)^{-1}-0,5}{2(x-5)^{-1}-1}\leq 0;$

$\frac{1,5}{2(x-5)^{-1}-1}\leq 0;$

$2(x-5)^{-1}-1< 0;$

$\frac{2}{x-5}-1< 0;$

$\frac{2-x+5}{x-5}< 0;$

$\frac{7-x}{x-5}<0;$

uyh

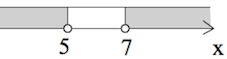
$x\in (-\infty;5)\cup(7;+\infty).$

Пересекаем решения неравенств (1) и (2):

Ответ: $[-1-2\sqrt6;0 )\cup (0;5).$

Смотрите также разбор заданий части В, С1(№15), С2(№16), С4(№18), С5(№20).

Возможно, вам будет интересно аналогичное задание смежного варианта:

Решите систему неравенств:

$\begin{cases} 1-\frac{4}{|x|}\leq \frac{20}{x^2},& & \frac{2-(x-6)^{-1}}{5(x-6)^{-1}-1}\leq -0,2; \end{cases}$

Ответ: + показать

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы