Главная › 14 (С3) Неравенства › С3 из тренировочной работы от 14 ноября 2013 (11 класс)

16 Ноя 2013

Категория: 14 (С3) НеравенстваЛогарифмыРациональные выражения, уравнения и неравенства

С3 из тренировочной работы от 14 ноября 2013 (11 класс)

Елена Репина 2013-11-16 2016-08-26

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Часть В тренировочной работы №1 (2013 г.) разобрана здесь.

Разбор задачи С3 из тренировочной работы в формате ЕГЭ 2014

Решите систему неравенств: $\begin{cases} log_{6x^2-x-1}(2x^2-5x+3)\geq 0,& & \frac{12x^2-31x+14}{4x^2+3x-1}\leq 0; \end{cases}$

Решение:

Решим по отдельности каждое неравенство. После чего пересечем множества их решений.

Неравенство (1):

Будем решать методом рационализации.

$log_{6x^2-x-1}(2x^2-5x+3)\geq 0\;\Leftrightarrow\; \begin{cases} (6x^2-x-1-1)(2x^2-5x+3-1)\geq 0,& & 6x^2-x-1>0,& &6x^2-x-1\neq 1,& & 2x^2-5x+3>0; \end{cases}$

$\begin{cases} (3x-2)(2x+1)(2x-1)(x-2)\geq 0,& &(2x-1)(3x+1)>0,& &(3x-2)(2x+1)\neq 0,& & (2x-3)(x-1)>0; \end{cases}$

На одной оси пересекаем множества решений каждой из строк системы:

шгр

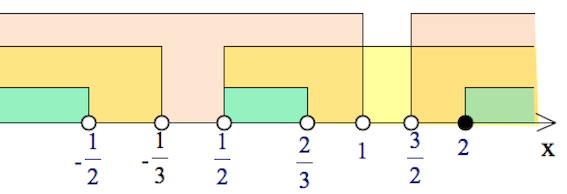
Получаем

$x\in (-\infty;-\frac{1}{2})\cup(\frac{1}{2};\frac{2}{3})\cup [2;+\infty).$

Неравенство (2):

Перепишем неравенство $\frac{12x^2-31x+14}{4x^2+3x-1}\leq 0$ следующим образом:

$12(x-\frac{7}{12})(x-2)\cdot 4(x+1)(x-\frac{1}{4})\leq 0,\;x\neq \frac{1}{4},\;x\neq -1;$

$(x-\frac{7}{12})(x-2)(x+1)(x-\frac{1}{4})\leq 0,\;x\neq \frac{1}{4},\;x\neq -1;$

$x\in (-1;\frac{1}{4})\cup[\frac{7}{12};2]$

Итак, пересекаем множества решений неравенств (1) и (2):

igb

$x\in(-1;-\frac{1}{2})\cup[\frac{7}{12};\frac{2}{3})\cup$ { $2$ }.

Ответ: $(-1;-\frac{1}{2})\cup[\frac{7}{12};\frac{2}{3})\cup$ { $2$ }.

Смотрите также С1(№15), С2(№16), С4(№18) тренировочной работы в формате ЕГЭ от 14 ноября 2013 года для 11 класса.

Для самостоятельной работы:

Решите систему неравенств: $\begin{cases} log_{6x^2+5x}(2x^2-3x+1)\geq 0,& & \frac{20x^2-32x+3}{3x^2+7x+2}\leq 0; \end{cases}$

Ответ: + показать

Автор: egeMax | Нет комментариев

Печать страницы

С3 из тренировочной работы от 14 ноября 2013 (11 класс)

Добавить комментарий Отменить ответ