С3 (№17) с логарифмами и модулями

Замечаем, что в первом неравенстве системы стоит два разных модуля. То есть нам придется раскрывать модули, рассматривать аж три неравенства (ведь у нас 3 промежутка, которые образуются нулями модулей – 5 и 6.)

Мы попытаем счастье – решим сначала второе неравенство системы, и, быть может, нам не придется проделывать лишнюю работу.

$\frac{1}{4}log_2(x-2)-\frac{1}{2}\leq log_{\frac{1}{4}}\sqrt{x-5};$

$\frac{1}{4}log_2(x-2)-log_{\frac{1}{4}}\sqrt{x-5}\leq \frac{1}{2};$

Так как $\frac{1}{4}=2^{-2}$, то, применяя 6-е свойство логарифмов, получаем:

$\frac{1}{4}log_2(x-2)+\frac{1}{2}log_2\sqrt{x-5}\leq \frac{1}{2};$

Домножаем обе части неравенства на 4:

$log_2(x-2)+2log_2\sqrt{x-5}\leq 2;$

Применяем свойствo 5, затем 3:

$log_2(x-2)(x-5)\leq 2,\;x>5;$

Обратите внимание, мы указали, что $x>5$, дабы не нарушить равносильный переход!

(Вы вполне можете решать неравенство, не соблюдая равносильные переходы, но тогда помните про ОДЗ).

Итак, представив $2$ как $log_24$, переходим к следующей строке, равносильной предыдущей:

$(x-2)(x-5)\leq 4,\;x>5;$

$x^2-7x+6\leq 0,\;x>5;$

$(x-6)(x-1)\leq 0,\;x>5$

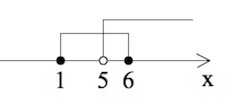
$x\in(5;6].$

Нам повезло! Мы как раз попали в один из промежутков, образованных нулями модулей из первого неравенства системы. Значит мы можем значительно сэкономить время, рассматривая первое неравенство лишь на  $(5;6].$

Итак,  на $(5;6]$ неравенство $\frac{|x-5|-1}{2|x-6|-4}\leq 1$ примет вид:

$\frac{x-5-1}{2(-x+6)-4}\leq 1;$

$\frac{x-6}{8-2x}-1\leq 1;$

$\frac{x-6-8+2x}{8-2x}\leq 0;$

$\frac{3x-14}{8-2x}\leq 0;$

$x\in(-\infty;4)\cup[\frac{14}{3};+\infty).$

Пересекая решения неравенств системы, получаем:

Ответ: $(5;6].$