29 Янв 2014

Категория: 16 (С4) Планиметр. задачиЕГЭ (диагностич. работы)Планиметрия

С4 (№18) Тренировочной работы от 28 января 2014 г.

Елена Репина 2014-01-29 2016-08-18

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также часть В Тренировочной работы от 28 января, а также С1(№15), С2(№16), С3(№17).

Две окружности пересекаются в точках $P$ и $Q$ . Прямая, проходящая через точку $P$ , второй раз пересекает первую окружность в точке $A$ , а вторую – в точке $D$ . Прямая, проходящая через точку $Q$ параллельно $AD$ , второй раз пересекает первую окружность в точке $B$ , а вторую – в точке $C$ .

а) Докажите, что четырёхугольник $ABCD$ – параллелограмм.

б) Найдите отношение $BP:PC$ , если радиус первой окружности вдвое больше радиуса второй.

Решение:

a) Для доказательства того, что $ABCD$ – параллелограмм, достаточно доказать, что $AB\parallel CD$ (ведь по условию $AD\parallel BC$ ). Докажем это.

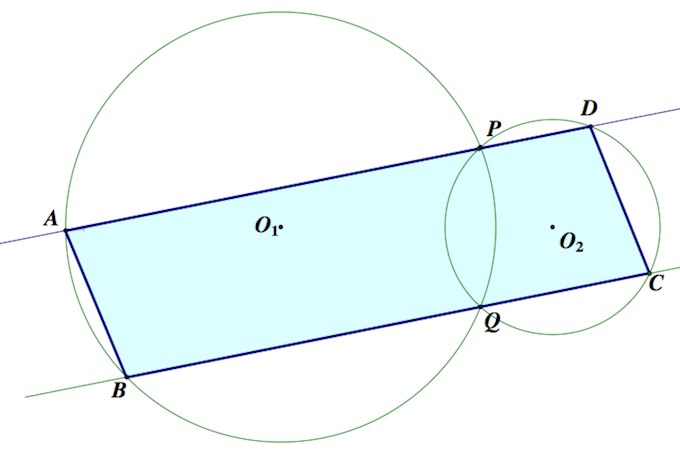
Трапеции $ABQP$ и $QPDC$ – равнобедренные, так как каждая из них вписана в окружность. Действительно, + показать

Тогда, очевидно, $\angle 1=\angle 2$ , $\angle 3=\angle 4$ , $\angle 5=\angle 6$ и $\angle 7=\angle 8$ (см. обозначения углов на рисунке). 87нр

Замечаем, что $(\angle 2+\angle 6)+(\angle 8+\angle 3)=180^{\circ}$ . Но тогда $(\angle 1+\angle 5)+(\angle 7+\angle 4)=180^{\circ}.$

Но ведь $\angle B=\angle 1+\angle 5$ и $\angle C=\angle 7+\angle 4$ –это внутренние односторонние углы при прямых $AB$ , $CD$ и секущей $BC$ . Раз они равны, то по признаку параллельности прямых $AB\parallel CD$ .

Итак, учитывая из условия параллельность прямых $AD$ и $BC$ , имеем – $ABCD$ – параллелограмм.

б) Докажем, что треугольники $BO_1P$ и $CO_2P$ (где $O_1,\;O_2$ – центры окружностей) подобны.

79п

Действительно,

$\angle BO_1P=360^{\circ}-2(\angle 2+\angle 6),$ (*)

так как $\angle BO_1P$ – это центральный угол, опирающийся на дугу, которую дуга $BAP$ , градусная мера которой вдвое больше градусной меры $\angle 2+\angle 6$ , дополняет до $360^{\circ}$ ).

При этом

$\angle PO_2C=2(\angle 8+\angle 3)$ (**)

как соответствующий центральный угол вписанного угла $PQC$ , равного $\angle 8+\angle 3$ .

А поскольку, по доказанному в п. а, $\angle 8+\angle 3+\angle 2 +\angle 6=180^{\circ}$ , то перепишем (**) так:

$\angle PO_2C=2(\angle 8+\angle 3)=360^{\circ}-2(\angle 2 +\angle 6)$ (***)

Сравнивая (*) и (***), видим, что $\angle BO_1P=\angle PO_2C.$

Этого достаточно для подобия треугольников $BO_1P$ и $CO_2P$ , так как они оба равнобедренные.

Но тогда, так как по условию $R:r=2:1$ (где $R,\;r$ – радиусы окружностей) а боковые стороны этих треугольников и есть соответственно $R$ и $r$ , то коэффициент подобия треугольников – 2.

Стало быть, и отношение соответствующих сторон подобных треугольников $BP:PC$ есть 2.

Ответ: 2.

Автор: egeMax | комментариев 8

Печать страницы

комментариев 8

Татьяна Бондаренко

2014-02-02 в 12:10

Отношение можно найти проще, если применить теорему синусов к треугольникам ABP и CDP: BP/sinB=2R, BC/sinD=2r, sinD=sinB , отсюда BP:PC=R:r=2.

[ Ответить ]
- egeMax
  
  2014-02-02 в 14:02
  
  Да, чуть-чуть быстрее :)
  А вообще, это расписывать все долго пришлось, а в принципе, конечно, подобие треугольников, о которых я говорила, очевидно.
  Спасибо! ;)
  
  [ Ответить ]
  - Марина
    
    2017-03-26 в 00:30
    
    Всегда ли подобны 2 равнобед треуг-и?
    
    [ Ответить ]
    - egeMax
      
      2017-03-26 в 08:32
      
      Два равнобедренных треугольника не обязаны быть подобными. Если есть у них две пары равных углов, то подобны по первому признаку подобия (по двум углам).
      
      [ Ответить ]
Максим

2015-03-30 в 14:04

а если бы не было известно, что AD параллельна BC, как тогда строилось бы доказательство?

[ Ответить ]
- egeMax
  
  2015-03-30 в 14:31
  
  Если бы, да кабы… Была бы другая задача… ;)
  
  [ Ответить ]
Димка

2016-08-18 в 18:46

В решении ошибка. В формуле (***) должен быть не угол PQC, а угол PO2C.

[ Ответить ]
- egeMax
  
  2016-08-18 в 20:31
  
  Димка, спасибо за замётанную опечатку – буквы $Q$ и $O_2$ так похожи…
  
  [ Ответить ]

С4 (№18) Тренировочной работы от 28 января 2014 г.

Добавить комментарий Отменить ответ