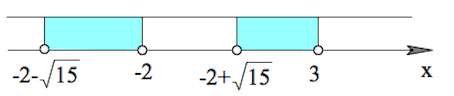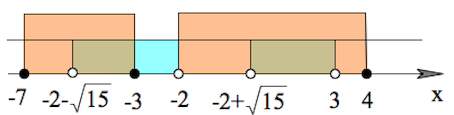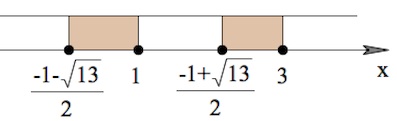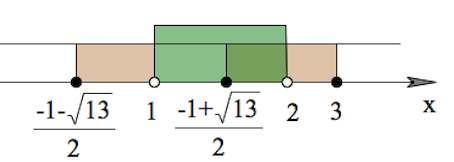Рассмотрим несколько примеров категории С3 (№15). Решать будем, используя метод рационализации
Пример 1. Решить неравенство $\frac{\sqrt{x^2+5x+6}-\sqrt{28-3x-x^2}}{x^2-x-6}<0$
Решение:+ показать
Находим ОДЗ неравенства:
$\begin{cases}x^2+5x+6\geq 0,\\28-3x-x^2\geq 0,\\x^2-x-6\neq 0;\end{cases}$
$\begin{cases}(x+2)(x+3)\geq 0,\\(x+7)(x-4)\leq 0,\\(x-3)(x+2)\neq 0;\end{cases}$
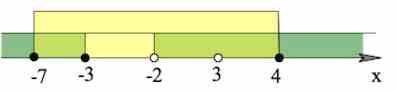
$x\in[-7;-3]\cup(-2;3)\cup(3;4]$.
Исходное неравенство будет иметь тоже решение, что и неравенство
$\frac{x^2+5x+6-28+3x+x^2}{x^2-x-6}<0$ на ОДЗ! согласно методу рационализации.
или
$(x^2+5x+6-28+3x+x^2)(x^2-x-6)<0$ (на ОДЗ)
$2(x^2+4x-11)(x-3)(x+2)<0$ (на ОДЗ)
$2(x-(-2+\sqrt{15}))(x-(-2-\sqrt{15}))(x-3)(x+2)<0$ (на ОДЗ)
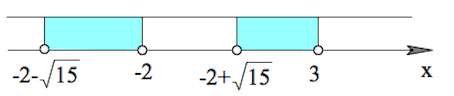
И, наконец, с учетом ОДЗ:
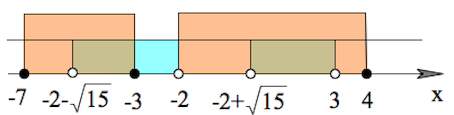
Ответ: $(-2-\sqrt{15};-3]\cup(-2+\sqrt{15};3)$.
Пример 2. Решить неравенство $\log_{\frac{x}{3}}(\log_x\sqrt{3-x})\geq 0$
Решение: + показать
ОДЗ данного неравенства:
$\begin{cases}\frac{x}{3}> 0,\\\frac{x}{3}\neq 1,\\\log_x\sqrt{3-x}>0,\\x>0,\\x\neq 1,\\\sqrt{3-x}>0;\end{cases}$
Производим преобразования, – они совсем несложные. А вот к третьей строке применяем метод замены множителей:
$\begin{cases}x> 0,\\x\neq 3,\\(x-1)(\sqrt{3-x}-1)>0,\\x\neq 1;\end{cases}$
И далее применяем рационализацию ко второй скобке в третьей строке:
$\begin{cases}x> 0,\\x\neq 3,\\(x-1)(3-x-1)>0,\\x\neq 1;\end{cases}$
$\begin{cases}x> 0,\\x\neq 3,\\(x-1)(2-x)>0,\\x\neq 1;\end{cases}$
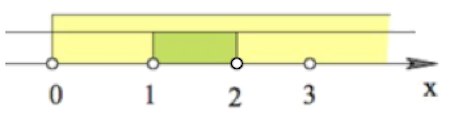
Возвращаемся к исходному неравенству
$\log_{\frac{x}{3}}(\log_x\sqrt{3-x})\geq 0$,
производим замену множителей:
$(\frac{x}{3}-1)(\log_x\sqrt{3-x}-1)\geq 0 $
И снова применяем метод замены множителей ко второму множителю:
$(\frac{x}{3}-1)(x-1)(\sqrt{3-x}-x)\geq 0$
К третьей скобке вновь применяем рационализацию.
Заметим, вообще говоря, $\sqrt{x^2}=|x|$, но так как в нашем случае (ОДЗ) $x>0,$ то $\sqrt{x^2}=x$, то есть $\sqrt{3-x}-x=\sqrt{3-x}-\sqrt{x^2}$.
$(\frac{x}{3}-1)(x-1)(3-x-x^2)\geq 0$
$-(\frac{x}{3}-1)(x-1)(x-\frac{-1+\sqrt{13}}{2})(x-\frac{-1-\sqrt{13}}{2})\geq 0$
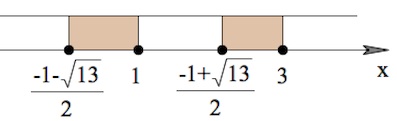
Учитываем ОДЗ:
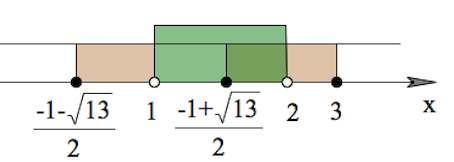
Ответ: $[\frac{-1+\sqrt{13}}{2};2)$.
Пример 3. Решить неравенство $x(|x^2-1|-2|x-1|)< 0$
Решение: + показать
Применяем метод рационализации:
$x(x^2-1-2(x-1))(x^2-1+2(x-1))<0$
$x(x^2-2x+1)(x^2+2x-3)<0$
$x(x-1)^2(x+3)(x-1)<0$
$x(x-1)^3(x+3)<0$
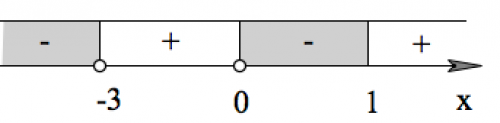
Ответ: $(-\infty;-3)\cup(0;1).$
Пример 4. Решить неравенство $\frac{4^{x^2+3x-2}-0,5^{2x^2+2x-1}}{5^x-1}\leq 0$
Решение: + показать
Представим $0,5^{2x^2+2x-1}$ как $((\frac{1}{2})^2)^{x^2+x-0,5}$,
то есть $0,5^{2x^2+2x-1}=(\frac{1}{4})^{x^2+x-0,5}$
Тогда
$\frac{4^{x^2+3x-2}-4^{-x^2-x+0,5}}{5^x-1}\leq 0$
или
$(4^{x^2+3x-2}-4^{-x^2-x+0,5})(5^x-1)\leq 0,$ $5^x\neq 1$
Применяем метод рационализации к каждой из скобок:
$(4-1)(x^2+3x-2+x^2+x-0,5)(5-1)(x-0)\leq 0,$ $x\neq 0$
$(2x^2+4x-2,5)x\leq 0,$ $x\neq 0$
$2x(x-0,5)(x+2,5)\leq 0,$ $x\neq 0$
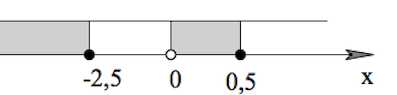
Ответ: $(-\infty;-2,5]\cup(0;0,5].$