Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Навигация (только номера заданий)
0 из 7 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Информация
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 7
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
Рубрики
- Нет рубрики 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- С ответом
- С отметкой о просмотре
-
Задание 1 из 7
1.
Найдите хорду, на которую опирается угол 90°, вписанный в окружность радиуса 38.
Правильно
76
Неправильно
76
-
Задание 2 из 7
2.
Найдите хорду, на которую опирается угол $120^{\circ}$, вписанный в окружность радиуса $22\sqrt3$.
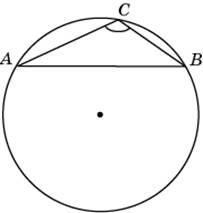Правильно
66
Неправильно
66
-
Задание 3 из 7
3.
Хорда AB делит окружность на две части, градусные величины которых относятся как 11:61. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
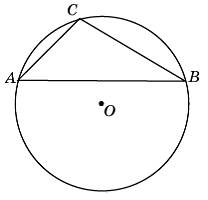Правильно
152,5
Неправильно
152,5
-
Задание 4 из 7
4.
Хорда AB стягивает дугу окружности в 64°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
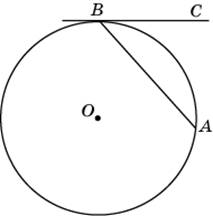Правильно
32
Неправильно
32
-
Задание 5 из 7
5.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.
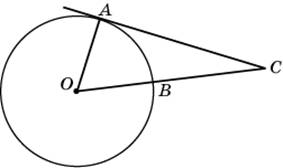Правильно
53
Неправильно
53
-
Задание 6 из 7
6.
Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
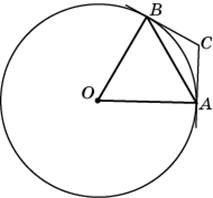Правильно
118
Неправильно
118
-
Задание 7 из 7
7.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
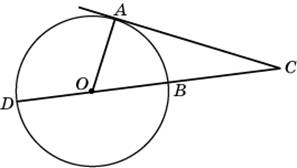Правильно
62
Неправильно
62
не понятен принцип решения 2-
Анатолий, соедините точки А и B с центром окружности. В полученном треугольнике (каков его вид?) вам известны две стороны и угол между ними (чему он равен?)…
Если подсказки не помогли пока, спрашивайте еще… Но, надеюсь, все получится у вас!
спасибо большое, всё понял ;)
Несколько раз перерешал, в 10-й задаче у меня получается …
И вы правы!
Была ошибка в ответе теста… ;(
Анатолий, в знак благодарности (а ведь на вашем счету не одна замеченная опечатка ;)) хочу вам сделать небольшой подарок! Вы получите 100 рублей на свой мобильный. Оставьте прям здесь свой номер (конечно, не опубликую…)
8-952-*******
Енисейтелеком?
да да да :)
Отправлено! :) :) :)
в условии 8-й задачи сказано найти величину большей дуги AD, заключенной внутри угла, но на самом деле внутри угла заключена меньшая дуга AD, и в ответе получается ***, то есть меньшая дуга :)
Анатолий, я сама, когда писАла задачу, внутренне сопротивлялась условию. Считаю, что составлена некорректно:
Угол ACO равен 16˚. Его сторона CA касается окружности. Найдите градусную величину большей дуги окружности AD, заключенной внутри этого угла. Ответ дайте в градусах.
Но взято из открытого банка заданий ЕГЭ по математике… Я поставлю дугу AD в скобки, – тогда все будет на своих местах (как бы уточнение сказанного тогда получается…)
Я имел ввиду, что многим может показаться что ответ не ***, а ***, так как в условии сказано найти БОЛЬШУЮ дугу…
Я вас поняла сразу. Но большая дуга AD уже не заключена внутри угла… Вот такое вот противоречие…
Вот такая формулировка теперь получается:
Угол ACO равен 16˚. Его сторона CA касается окружности. Найдите градусную величину большей дуги окружности, заключенной внутри этого угла (AD). Ответ дайте в градусах.
P.S. Надеюсь, в таком виде
Угол ACO равен 16˚. Его сторона CA касается окружности. Найдите градусную величину большей дуги окружности AD, заключенной внутри этого угла. Ответ дайте в градусах.
составители на выставят задачу на ЕГЭ…При решении задания номер 10 (Из одной точки проведены к окружности касательная и секущая. AB=3 корней из 11, AD=18. Определить внутренний отрезок CD секущей.), обнаружил что задача не решается. Решение сводится к решению системы:
{AB^2=ACxCD
{18=AC+CD
и вот что получается –
{99=ACxCD
{18=AC+CD
выражаем AC, AC=99/CD
подставив получается уравнение которое не решается –
CD^2-18CD+99=0
D<0
нет корней…
[latexpage] Денис, ошибка ваша здесь: $AB^2=AC\cdot CD$.
Загляните сюда.