Разбор заданий 13-18 Тренировочной работы
13. Дано уравнение $sin(134\pi-15x)+sin(90x+\frac{135\pi}{2})=2$
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие промежутку $[-\frac{3\pi}{7};\frac{3\pi}{8}].$
Решение: + показать
а)
$sin(134\pi-15x)+sin(90x+\frac{135\pi}{2})=2;$
$-sin15x-cos90x=2;$
Так как $|sin15x|\leq 1$ и $|cos90x|\leq 1$, то равенство возможно только в случае $sin15x=cos90x=-1$.
$\begin{cases}sin15x=-1,\\cos90x=-1;&\end{cases}$
$\begin{cases}15x=-\frac{\pi}{2}+2\pi n,n\in Z,\\90x=\pi+ 2\pi k,k\in Z;&\end{cases}$
$\begin{cases}x=-\frac{\pi}{30}+\frac{2\pi n}{15},n\in Z,\\x=\frac{\pi}{90}+\frac{\pi k}{45},k\in Z;&\end{cases}$
Откуда
$-\frac{\pi}{30}+\frac{2\pi n}{15}=\frac{\pi}{90}+\frac{\pi k}{45},n,k\in Z;$
$-3+12n=1+2k,k\in Z;$
$12n-4=2k,k\in Z;$
$6n-2=k,k\in Z;$
Итак,
$x=\frac{\pi}{90}+\frac{\pi (6n-2)}{45},n\in Z;$
$x=\frac{\pi}{90}-\frac{2\pi}{45}+\frac{2\pi n}{15},n\in Z;$
$x=-\frac{\pi}{30}+\frac{2\pi n}{15},n\in Z.$
б) Произведем отбор корней.
$-\frac{3\pi}{7}\leq -\frac{\pi}{30}+\frac{2\pi n}{15}\leq \frac{3\pi}{8},n\in Z;$
$-\frac{3}{7}\leq -\frac{1}{30}+\frac{2n}{15}\leq \frac{3}{8},n\in Z;$
$-360\leq -28+112n\leq 315,n\in Z;$
$-332\leq 112n\leq 343,n\in Z;$
$-\frac{332}{112}\leq n\leq \frac{343}{112},n\in Z;$
$-2\frac{108}{112}\leq n\leq 3\frac{7}{112},n\in Z;$
$n\in ${$-2;-1;0;1;2;3$}.
Тогда на указанном отрезке располагаются следующие корни:
при $n=-2$ $x=-\frac{\pi}{30}-\frac{4\pi}{15}=-\frac{\pi}{30}-\frac{8\pi}{30}=-\frac{3\pi}{10};$
при $n=-1$ $x=-\frac{\pi}{30}-\frac{2\pi}{15}=-\frac{\pi}{30}-\frac{4\pi}{30}=-\frac{\pi}{6};$
при $n=0$ $x=-\frac{\pi}{30};$
при $n=1$ $x=-\frac{\pi}{30}+\frac{2\pi}{15}=-\frac{\pi}{30}+\frac{4\pi}{30}=\frac{\pi}{10};$
при $n=2$ $x=-\frac{\pi}{30}+\frac{4\pi}{15}=-\frac{\pi}{30}+\frac{8\pi}{30}=\frac{7\pi}{30};$
при $n=3$ $x=-\frac{\pi}{30}+\frac{6\pi}{15}=-\frac{\pi}{30}+\frac{12\pi}{30}=\frac{11\pi}{30};$
Ответ:
а) $-\frac{\pi}{30}+\frac{2\pi n}{15},n\in Z.$
б) $-\frac{3\pi}{10};-\frac{\pi}{6};-\frac{\pi}{30};\frac{\pi}{10};\frac{7\pi}{30};\frac{11\pi}{30}.$
14. Все рёбра куба $ABCDA_1B_1C_1D_1$ равны $\sqrt{134}$.
а) Постройте сечение куба, проходящее через середины рёбер $AB$, $BC$, $CC_1$.
б) Найдите площадь этого сечения.
Решение: + показать
a) Пусть $M,N,P$ – середины $AB,BC$ и $CC_1$ соответственно.
Пусть прямая $MN$ пересекается с прямыми $AD,DC$ в точках $E$ и $F$.
Пусть $PF$ пересекается с $D_1C_1$ в точке $Q$.
Пусть $NP$ пересекается с $B_1C_1$ в точке $L$.
Пусть $QL$ пересекается с $A_1D_1$ в точке $T$.
Наконец, пусть $TE$ пересекается с $AA_1$ в точке $S$.
Шестиугольник $MNPQTS$ – искомое сечение.
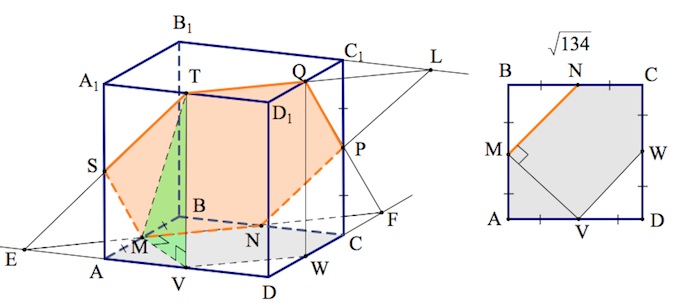
б)
$S_{MNPQTS}=\frac{S_{MNCWVA}}{cos\alpha}$, где $S_{MNCWVA}$ – площадь проекции шестиугольника $MNPQTS$ на плоскость основания, $\alpha –$ угол между плоскостями сечения и основания.
Несложно заметить (по построению), что точки $T,Q$ и $S$ – середины ребер $A_1D_1,D_1C_1,AA_1$ соответственно.
Точка $V,$ проекция $T$ на плоскость $ABC$ также середина ребра $AD$. Тогда, очевидно, $VM\perp MN$. По теореме о трех перпендикулярах и $MT\perp MN$. Итак, $\alpha=\angle TMV$ – угол между плоскостями сечения и основания.
Далее,
$S_{MNCWVA}=S_{ABCD}-2S_{VWD}=(\sqrt{134})^2-2\cdot (\frac{(\frac{\sqrt{134}}{2})^2}{2})^2=\frac{201}{2}.$
$cos\alpha =\frac{MV}{MT}=\frac{\sqrt{67}}{\sqrt{67\cdot 3}}=\frac{1}{\sqrt3}.$
Наконец, $S_{MNPQTS}=\frac{\frac{201}{2}}{\frac{1}{\sqrt3}}=\frac{201\sqrt3}{2}.$
Ответ: б) $\frac{201\sqrt3}{2}.$
15. Решите неравенство $\frac{1}{2}log_{134+tg^2(\frac{x}{2})}(21x+16)<log_{134+tg^2(\frac{x}{2})}(20+\sqrt{x-4}).$
Решение: + показать
$\frac{1}{2}log_{134+tg^2(\frac{x}{2})}(21x+16)<log_{134+tg^2(\frac{x}{2})}(20+\sqrt{x-4});$
$log_{134+tg^2(\frac{x}{2})}\sqrt{21x+16}<log_{134+tg^2(\frac{x}{2})}(20+\sqrt{x-4});$
$(134+tg^2(\frac{x}{2})-1)(\sqrt{21x+16}-(20+\sqrt{x-4}))<0;$
$(133+tg^2(\frac{x}{2}))(\sqrt{21x+16}-\sqrt{x-4}-20)<0;$
$\sqrt{21x+16}-\sqrt{x-4}-20<0,\frac{x}{2}\neq \frac{\pi}{2}+\pi n, n\in Z;$
$\sqrt{21x+16}<20+\sqrt{x-4},x\neq \pi+2\pi n, n\in Z;$
$0\leq 21x+16<400+40\sqrt{x-4}+x-4,x\neq \pi+2\pi n, n\in Z;$
$\begin{cases}x\geq -\frac{16}{21},\\20x-380<40\sqrt{x-4},\\x\neq \pi+2\pi n, n\in Z;&\end{cases}$
$\begin{cases}x\geq -\frac{16}{21},\\x-19<2\sqrt{x-4},\\x\neq \pi+2\pi n, n\in Z;&\end{cases}$
$\begin{cases}x\geq -\frac{16}{21},\\\left[\begin{array}{cl}\begin{cases}x-19<0,\\x-4\geq 0;\end{cases}\\\begin{cases}x-19\geq 0,\\x^2-38x+361<4(x-4);\end{cases}\end{array}\right.\\x\neq \pi+2\pi n, n\in Z;&\end{cases}$
$\begin{cases}x\geq -\frac{16}{21},\\\left[\begin{array}{cl}4\leq x<19;\\\begin{cases}x\geq 19,\\x^2-42x+377<0;\end{cases}\end{array}\right.\\x\neq \pi+2\pi n, n\in Z;&\end{cases}$
$\begin{cases}x\geq -\frac{16}{21},\\\left[\begin{array}{cl}4\leq x<19;\\\begin{cases}x\geq 19,\\(x-29)(x-13)<0;\end{cases}\end{array}\right.\\x\neq \pi+2\pi n, n\in Z;&\end{cases}$
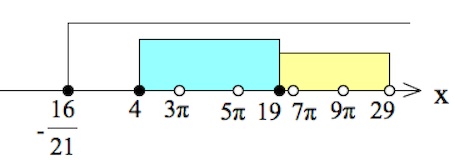
$x\in [4;3\pi)\cup (3\pi;5\pi)\cup (5\pi;7\pi)\cup (7\pi;9\pi)\cup (9\pi;29).$
Ответ: $[4;3\pi)\cup (3\pi;5\pi)\cup (5\pi;7\pi)\cup (7\pi;9\pi)\cup (9\pi;29).$
16. Даны треугольники $ABC$ и $A_1B_1C_1$. Прямые $AA_1,BB_1, CC_1$ пересекаются в одной точке. Прямые $AB$ и $A_1B_1$ пересекаются в точке $C_2.$ Прямые $AC$ и $A_1C_1$ пересекаются в точке $B_2$. Прямые $BC$ и $B_1C_1$ пересекаются в точке $A_2$.
а) Докажите, что точки $A_2,B_2,C_2$ лежат на одной прямой.
б) Найдите отношение площади треугольника $A_1B_1C_1$ к площади треугольника $ABC$, если высоты треугольника $ABC$ равны $2,\frac{10}{11},\frac{5}{7}$, а высоты треугольника $A_1B_1C_1$ равны $2,\frac{5}{3},\frac{10}{9}.$
Решение: + показать
а) По теореме Менелая для треугольника $C_1OA_1$ и прямой $CA$
$\frac{C_1C}{CO}\cdot \frac{OA}{AA_1}\cdot \frac{A_1B_2}{B_2C_1}=1$ (1)
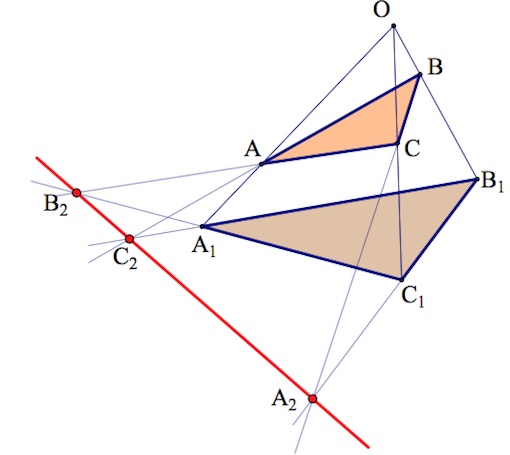
По теореме Менелая для треугольника $C_1OB_1$ и прямой $CB$
$\frac{C_1C}{CO}\cdot \frac{OB}{BB_1}\cdot \frac{B_1A_2}{A_2C_1}=1$ (2)
По теореме Менелая для треугольника $B_1OA_1$ и прямой $BA$
$\frac{B_1B}{BO}\cdot \frac{OA}{AA_1}\cdot \frac{A_1C_2}{C_2B_1}=1$ (3)
Разделим (1) на (2) и на (3):
$\frac{C_1C}{CO}\cdot \frac{OA}{AA_1}\cdot \frac{A_1B_2}{B_2C_1}\cdot \frac{CO}{C_1C}\cdot \frac{BB_1}{OB}\cdot \frac{A_2C_1}{B_1A_2}\cdot \frac{BO}{B_1B}\cdot \frac{AA_1}{OA}\cdot \frac{C_2B_1}{A_1C_2}=1;$
$\frac{A_1B_2}{B_2C_1}\cdot \frac{C_1A_2}{A_2B_1}\cdot \frac{B_1C_2}{C_2A_1}=1.$
По теореме Менелая из последнего равенства следует, что точки $A_2, B_2,C_2$ лежат на одной прямой.
б) Пусть $AB=c,BC=a,AC=b,A_1B_1=c_1,B_1C_1=a_1,A_1C_1=b_1.$
Пусть $h_a=2,h_b=\frac{10}{11},h_c=\frac{5}{7},h_{a_1}=2,h_{b_1}=\frac{5}{3},h_{c_1}=\frac{10}{9}$.
Тогда
$a=\frac{2S_{ABC}}{2}=S_{ABC};$
$b=\frac{2S_{ABC}}{\frac{10}{11}}=\frac{11}{5}S_{ABC};$
$c=\frac{2S_{ABC}}{\frac{5}{7}}=\frac{14}{5}S_{ABC};$
$a_1=\frac{2S_{A_1B_1C_1}}{2}=S_{A_1B_1C_1};$
$b_1=\frac{2S_{A_1B_1C_1}}{\frac{5}{3}}=\frac{6}{5}S_{A_1B_1C_1};$
$c_1=\frac{2S_{A_1B_1C_1}}{\frac{10}{9}}=\frac{9}{5}S_{A_1B_1C_1}.$
Получаем тогда
$p_{ABC}=\frac{S_{ABC}+\frac{11}{5}S_{ABC}+\frac{14}{5}S_{ABC}}{2}=3S_{ABC};$
$p_{A_1B_1C_1}=\frac{S_{A_1B_1C_1}+\frac{6}{5}S_{A_1B_1C_1}+\frac{9}{5}S_{A_1B_1C_1}}{2}=2S_{A_1B_1C_1}.$
Далее, по формуле Герона
$S_{ABC}=\sqrt{p_{ABC}(p_{ABC}-a)(p_{ABC}-b)(p_{ABC}-c)};$
$S^2_{ABC}=3S_{ABC}(3S_{ABC}-S_{ABC})(3S_{ABC}-\frac{11}{5}S_{ABC})(3S_{ABC}-\frac{14}{5}S_{ABC});$
$S^2_{ABC}=\frac{24}{25}S^4_{ABC};$
$S_{ABC}=\frac{5}{2\sqrt6}.$
И
$S_{A_1B_1C_1}=\sqrt{p_{A_1B_1C_1}(p_{A_1B_1C_1}-a_1)(p_{A_1B_1C_1}-b_1)(p_{A_1B_1C_1}-c_1)};$
$S^2_{A_1B_1C_1}=2S_{A_1B_1C_1}(S_{A_1B_1C_1})(2S_{A_1B_1C_1}-\frac{6}{5}S_{A_1B_1C_1})(2S_{A_1B_1C_1}-\frac{9}{5}S_{A_1B_1C_1});$
$S^2_{A_1B_1C_1}=\frac{8}{25}S^4_{A_1B_1C_1};$
$S_{A_1B_1C_1}=\frac{5}{2\sqrt{2}}.$
Итак,
$\frac{S_{A_1B_1C_1}}{S_{ABC}}=\frac{\frac{5}{2\sqrt{2}}}{\frac{5}{2\sqrt6}}=\sqrt3.$
Ответ: б) $\sqrt3.$
17. Баржа грузоподъёмностью $134$ тонны перевозит контейнеры типов A и B. Количество загруженных на баржу типа B не менее чем на 25% превосходит загруженных контейнеров типа A. Вес и стоимость одного контейнера типа A составляет $2$ тонны и $5$ млн. руб., контейнера типа B – $5$ тонн и $7$ млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Решение: + показать
Пусть количество загруженных на баржу типа А контейнеров – $x$ штук.
Пусть количество загруженных на баржу типа B контейнеров – $y$ штук.
Суммарная стоимость (в млн. руб.) $S$ всех контейнеров, перевозимых баржей тогда составит $5x+7y$.
Откуда
$x=\frac{S-7y}{5}$ (1)
Так как грузоподъемность баржи $134$ тонны, то
$2x+5y \leq 134$;
С учетом (1) имеем:
$2\cdot \frac{S-7y}{5}+5y\leq 134;$
$2S-14y+25y\leq 670;$
$2S+11y\leq 670;$
$11y\leq 670-2S$ (2)
Заметим, согласно условию, $y\geq 1,25x.$
Тогда
$y\geq \frac{5}{4}\cdot \frac{S-7y}{5};$
$11y\geq S$ (3)
Учитывая (2) и (3), получаем
$S\leq 11y\leq 670-2S;$
$S\leq 670-2S;$
$3S\leq 670;$
$S\leq 223\frac{1}{3};$
Если $S=223$, то $223\leq 11y\leq 224$ или $20\frac{3}{11}\leq y\leq 20\frac{4}{11}.$ Так как $y$ – натуральное, то решений в этом случае нет.
Если $S=222$, то $222\leq 11y\leq 226$ или $20\frac{2}{11}\leq y\leq 20\frac{6}{11}.$ Так как $y$ – натуральное, то решений в этом случае нет.
Если $S=221$, то $221\leq 11y\leq 228$ или $20\frac{1}{11}\leq y\leq 20\frac{8}{11}.$ Так как $y$ – натуральное, то решений в этом случае нет.
Если $S=220$, то $220\leq 11y\leq 230$ или $20\leq y\leq 20\frac{10}{11}.$ Так как $y$ – натуральное, то $y=20.$
Итак, если имеется $20$ контейнеров типа В и $16$ типа А, то суммарная стоимость всех контейнеров, перевозимых баржей, составит $220$ млн. рублей.
Ответ: $220.$
Аналогичная задача здесь
18. Найдите все значения $a$, при каждом из которых неравенство
$log_{2}^3x-3\log^2_2x<(134+a)log_2x$
выполняется для любых $x\in [2;4\sqrt2].$
Решение: + показать
Примем $log_2x$ за $m$.
Тогда будем искать все значения $a$, при каждом из которых неравенство
$m^3-3m^2<(134+a)m$
выполняется для любых $m\in [1;2,5].$
Иммеем
$m(m^2-3m-(134+a))<0;$
$m(m-\frac{3-\sqrt{545+4a}}{2})(m-\frac{3+\sqrt{545+4a}}{2})<0;$
В зависимости от параметра $a$ корни $0;\frac{3\pm \sqrt{545+4a}}{2}$ могут по-разному располагаться на оси.
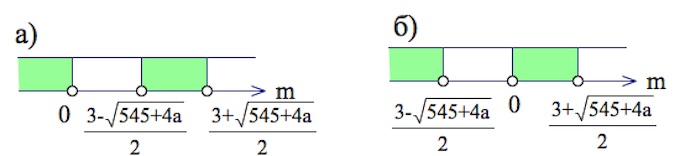
Для варианта а) потребуем, чтобы $[1;2,5]$ входил бы в $(\frac{3-\sqrt{545+4a}}{2};\frac{3+\sqrt{545+4a}}{2})$.
Для варианта б) потребуем, чтобы $[1;2,5]$ входил бы в $(0;\frac{3+\sqrt{545+4a}}{2})$.
Итак,
$\left[\begin{array}{rcl}\begin{cases}\frac{3-\sqrt{545+4a}}{2}<1,\\\frac{3+\sqrt{545+4a}}{2}>2,5;\end{cases}\\\frac{3+\sqrt{545+4a}}{2}>2,5;\end{array}\right.$
$\left[\begin{array}{rcl}\sqrt{545+4a}>1,\\\sqrt{545+4a}>2;\end{array}\right.$
$\sqrt{545+4a}>2;$
$545+4a>4;$
$4a>-541;$
$a>-135,25.$
Ответ: $(-135,25;+\infty).$





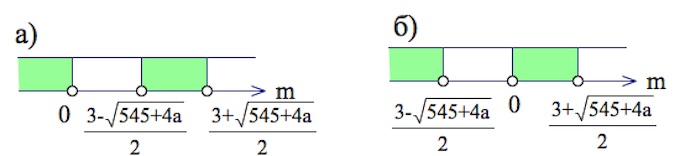
В задаче 14 можно доказать, что правильный шестиугольник со стороной квадратный корень из 134 /2 и найти площадь сечения . гораздо проще
Елена, в задаче 14 на выносном чертеже точки N и W поменяны местами. Поправьте, пожалуйста.
Людмила, спасибо большое!
Здравствуйте. Возможно ли такое решение для задачи 17? Поскольку конт. А перевозить выгоднее (5/2=2,5 млн/т против 7/5=1,4 млн/т), то следует загрузить их как можно больше, а конт. В как можно меньше, т.е. ровно 5/4 от А. Получим систему из неравенства и уравнения 2А+5В</=134 и В=5А/4. Решив ее, получим А</=16+(8/33). Наибольшее целое значение А=16. Таким образом, следует погрузить 16 конт. А и 20 конт. В. Стоимость будет 220 млн руб., но баржа пойдет с недогрузом в 2 тонны. Проверим, как изменится стоимость груза, если увеличить число конт. В и загрузить баржу полностью. Если загрузить 12 конт. А и 22 В, то 12*2+22*5=134 т – баржа полностью загружена, но стоимость перевозимого груза понизится 12*5+22*7=214 млн руб. Ответ: 220 млн руб.