Тренировочная работа №141 А. Ларина

a)

$\large\frac{1-4cosx}{3+4cosx}=tg^2x;$

$\large\frac{1-4cosx}{3+4cosx}=\frac{sin^2x}{cos^2x};$

$\begin{cases}(1-4cosx)cos^2x=(3+4cosx)(1-cos^2x),\\3+4cosx\neq 0,\\cosx\neq 0;&\end{cases}$

$\begin{cases}cos^2x-4cos^3x=3-3cos^2x+4cosx-4cos^3x,\\cosx\neq -\frac{3}{4},\\cosx\neq 0;&\end{cases}$

$\begin{cases}4cos^2x-4cosx-3=0,\\cosx\neq -\frac{3}{4},\\cosx\neq 0;&\end{cases}$

$\begin{cases}cosx=-\frac{1}{2},\\cosx\neq -\frac{3}{4},\\cosx\neq 0;&\end{cases}$

$cosx=-\frac{1}{2};$

$x=\pm \frac{2\pi}{3}+2\pi n, n\in Z.$

б) Корни уравнения, принадлежащих интервалу $[\frac{3\pi}{4}; 3\pi]:$

$x=\frac{4\pi}{3}$, $x=\frac{8\pi}{3}.$

Ответ:

а) $\pm \frac{2\pi}{3}+2\pi n, n\in Z.$

б) $\frac{4\pi}{3}$, $\frac{8\pi}{3}.$

a) Пусть $O_1,O$ – центры верхнего и нижнего оснований соответственно, $N,P$ – середины ребер $AC,AB.$

$\beta =(O_1NP).$

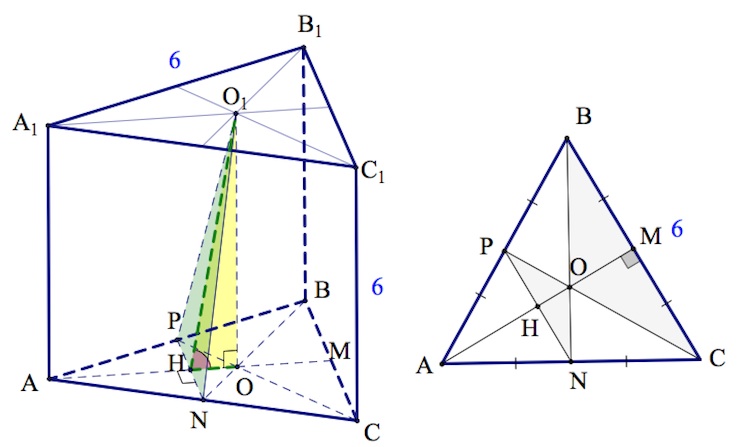
$OO_1\perp (ABC)$.

Пусть $H$ – середина $NP$.

$OH\perp NP$.

По теореме о трех перпендикулярах и $O_1H\perp NP$.

Итак, $\angle (\beta;(ABC))=\angle O_1HO.$

Пусть ребро призмы – $a$.

Очевидно, $OO_1=a$.

Далее, из подобия треугольников $PON,COB$ с коэффициентом подобия $1/2$, получаем, что $OH=\frac{OM}{2}$ (где $M$ – середина $BC$), при этом $OM=\frac{AM}{3}$ по свойству медиан.

Итак,

$OH=\frac{AM}{6}=\frac{\sqrt{a^2-(\frac{a}{2})^2}}{6}=\frac{a\sqrt3}{12}.$

$tgO_1HO=\frac{OO_1}{OH}=\frac{a}{\frac{a\sqrt3}{12}}=4\sqrt3.$

$\angle (\beta;(ABC))=\angle O_1HO=arctg(4\sqrt3).$

б) Построим сечение призмы плоскостью $\beta$. Прежде следует построить через $O_1$ прямую, параллельную $PN$ (или $B_1C_1$), ведь параллельные плоскости пересекаются третьей по параллельным прямым. Для этого отметим точки $E,F$ на прямых $A_1B_1,A_1C_1$ так, что $A_1E:A_1B_1=2:3$ и $A_1F:A_1C_1=2:3$. Прямая $EF$ и будет той прямой, по которой $\beta $ пересечет плоскость верхнего основания призмы (треугольники $A_1EF, A_1B_1C_1$ подобны, коэффициент подобия – $\frac{2}{3}$).

Трапеция $EFNP$ – искомое сечение. Найдем площадь трапеции $EFNP$ через площадь ее проекции на $ABC.$

Пусть $T,S$ – проекции $E,F$ на плоскость $ABC$.

Тогда $S_{EFNP}=\frac{S_{TSNP}}{cos\alpha}$, где $\alpha$ – угол между плоскостями $\beta $ и $(ABC)$, найденный в пункте (а).

Найдем $cos\alpha$, зная $tg\alpha$.

$cos^2\alpha =\frac{1}{1+tg^2\alpha }=\frac{1}{1+48}=\frac{1}{49}.$

Откуда $cos\alpha =\frac{1}{7}.$

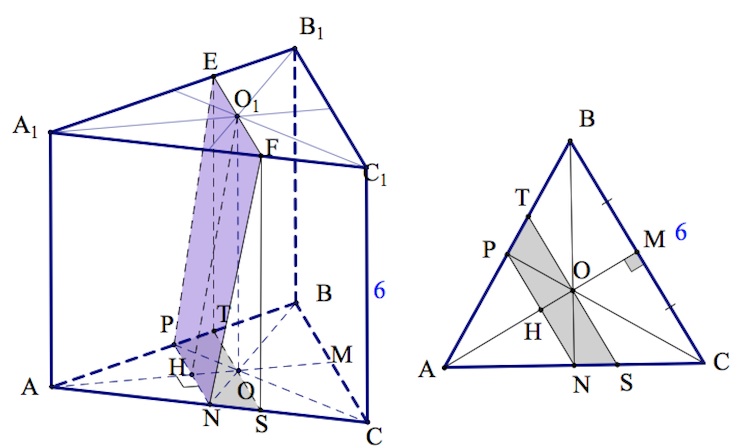
Далее,

$S_{APN}=\frac{S_{ABC}}{4}$ (треугольники $APN, ABC$  подобны и коэффициент подобия равен $\frac{1}{2}$).

$S_{ATS}=\frac{4}{9}\cdot S_{ABC}$ (треугольники $ATS, ABC$  подобны и коэффициент подобия равен $\frac{2}{3}$).

$S_{TSNP}=S_{ATS}-S_{APN}=\frac{4}{9}\cdot S_{ABC}-\frac{S_{ABC}}{4}=\frac{7}{36}\cdot S_{ABC}.$

При этом $S_{ABC}=\frac{a^2\sqrt3}{4}=9\sqrt3$ (при $a=6$).

 Итак, $S_{EFNP}=\frac{S_{TSNP}}{cos\alpha}=\frac{\frac{7\sqrt3}{4}}{\frac{1}{7}}=\frac{49\sqrt3}{4}.$

Ответ: 

а) $arctg(4\sqrt3);$

б) $\frac{49\sqrt3}{4}.$

$log_x(log_2(4^x-6))-log_xx\leq 0;$

Применяем метод замены множителей.

$\begin{cases}(x-1)(log_2(4^x-6)-x)\leq 0,\\log_2(4^x-6)>0,\\x>0,\\x\neq 1;&\end{cases}$

Опять применяем метод замены множителей (к первой, второй строкам системы).

$\begin{cases}(x-1)(2-1)(4^x-6-2^x)\leq 0,\\(2-1)(4^x-6-1)>0,\\4^x-6>0,\\x>0,\\x\neq 1;&\end{cases}$

$\begin{cases}(x-1)(4^x-2^x-6)\leq 0,\\4^x>7,\\4^x>6,\\x>0,\\x\neq 1;&\end{cases}$

$\begin{cases}(x-1)(2^x-3)(2^x+2)\leq 0,\\4^x>7,\\4^x>6,\\x>0,\\x\neq 1;&\end{cases}$

К первой строке вновь применяется метод замены множителей.

$\begin{cases}(x-1)(2^x-2^{log_23})\leq 0,\\4^x>4^{log_47},\\4^x>6,\\x>0,\\x\neq 1;&\end{cases}$

$\begin{cases}(x-1)(x-log_23)\leq 0,\\x>log_47,\\4^x>6,\\x>0,\\x\neq 1;&\end{cases}$

Заметим, $1<log_47=log_2\sqrt7<log_23.$

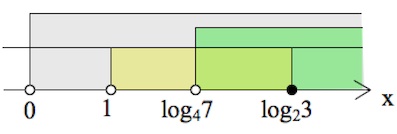
$x\in (log_47;log_23].$

Ответ: $(log_47;log_23].$ 

a) Пусть сторона ромба $ABCD$ – $a$, радиус вписанной окружности – $r$.

Замечаем, что высота ромба – диаметр вписанной окружности.

$S_{ABCD}=a\cdot 2r.$

$S_{\Theta }=\pi r^2.$

Покажем, что $S_{\Theta }<0,8\cdot S_{ABCD}.$

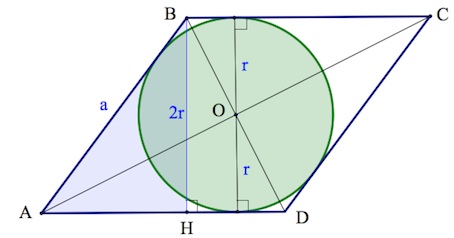
Рассмотрим разность $S_{\Theta }-0,8\cdot S_{ABCD}.$

При решении используем тот факт, что $2r<a$ (катет меньше гипотенузы, из $\Delta ABH$, см. рис.).

Тогда

$S_{\Theta }-0,8\cdot S_{ABCD}=\pi r^2-0,8\cdot a\cdot 2r<\pi r^2-0,8\cdot 4r^2=r^2(\pi-3,2)<0.$

Итак, $S_{\Theta }<0,8\cdot S_{ABCD}$. Это и  означает, что площадь круга, ограниченного окружностью $\Theta $, составляет менее $80$% площади ромба.

б) Пусть $O,O_1,O_2$ – центры окружностей $\Theta, \omega_1,\omega_2$  соответственно.

Пусть $H,H_1,H_2$ – точки касания окружностей $\Theta, \omega_1,\omega_2$ со стороной $DC$ соответственно.

Пусть $r_1,r_2$ – радиусы окружностей $\omega_1,\omega_2$ соответственно.

Пусть $OD:OC=1:2.$

Поскольку $OC=2OD$ (то есть $tgOCD=\frac{1}{2}$), то и $H_1C=2O_1H_1=2r_1.$ Аналогично $DH_2=\frac{O_2H_2}{2}=\frac{r_2}{2}.$

Тогда $O_1C=r_1\sqrt5, O_2D=\frac{r_2\sqrt5}{2}$  (из треугольников $O_1CH_1,O_2DH_2$ по теореме Пифагора).

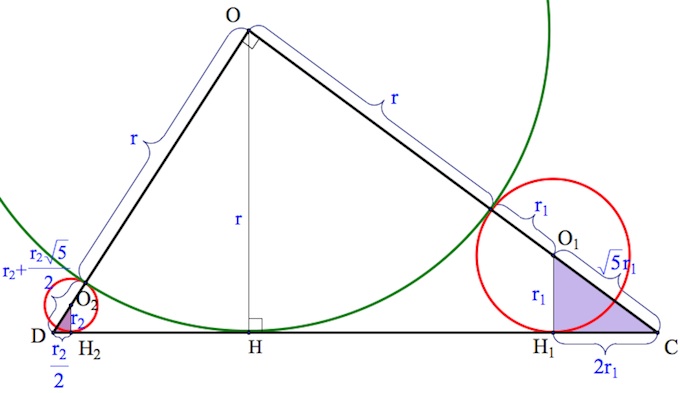
Из подобия треугольников $OHC,O_1H_1C$ следует: $\frac{r}{r_1}=\frac{r+r_1(1+\sqrt5)}{r_1\sqrt5}.$

Откуда

$r=\frac{r_1(\sqrt5+1)}{\sqrt5-1}$  

$r=\frac{r_1(3+\sqrt5)}{2}$   (1)

Еще раз используем, что $OC:OD=2$, получаем

$r+r_1(1+\sqrt5)=2(r+r_2(1+\frac{\sqrt5}{2}))$

или

$r=r_1(1+\sqrt5)-2r_2(1+\frac{\sqrt5}{2})$  (2)

Подставляя (1) в (2), получаем

$\frac{r_1(3+\sqrt5)}{2}=r_1(1+\sqrt5)-2r_2(1+\frac{\sqrt5}{2});$

$r_1(1+\sqrt5-\frac{3+\sqrt5}{2})=2r_2(1+\frac{\sqrt5}{2});$

$\frac{r_1(\sqrt5-1)}{2}=r_2(2+\sqrt5);$

$\large\frac{r_1}{r_2}=\frac{2+\sqrt5}{\frac{\sqrt5-1}{2}};$

$\large\frac{r_1}{r_2}=\frac{7+3\sqrt5}{2}.$

Ответ: $\frac{7+3\sqrt5}{2}.$

К концу первого месяца сумма на счету Эльвиры увеличится на $0,1\cdot 1$ млн. рублей. Эльвира должна выплатить $\frac{1}{36}$ кредита, а также покрыть сумму, на которую увеличился кредит за месяц.

То есть Эльвира должна внести к концу первого месяца сумму в

$0,1\cdot 1+\frac{1}{36}$

млн. рублей.

Теперь уже оставшаяся сумма (а именно $\frac{35}{36}$ млн. рублей) будет подвергаться воздействию $10$%. Прирост составит $0,1\cdot \frac{35}{36}$ млн. рублей.

Тогда Эльвира должна внести к концу второго месяца сумму в

$0,1\cdot \frac{35}{36}+\frac{1}{36}$

млн. рублей.

И так далее.

За первые $12$ месяцев, таким образом, Эльвира выплатит

$(0,1\cdot 1+\frac{1}{36})+(0,1\cdot \frac{35}{36}+\frac{1}{36})+…(0,1\cdot \frac{25}{36}+\frac{1}{36})$

млн. рублей.

Или

$0,1(1+\frac{35}{36}+…+\frac{24}{36})+\frac{12}{36}$

млн. рублей.

Аналогично за последние $12$ месяцев Эльвира выплатит

$(0,1\cdot \frac{12}{36}+\frac{1}{36})+(0,1\cdot \frac{11}{36}+\frac{1}{36})+…(0,1\cdot \frac{1}{36}+\frac{1}{36})$

млн. рублей.

Или

$0,1(\frac{12}{36}+\frac{11}{36}…+\frac{1}{36})+\frac{12}{36}$

млн. рублей.

Рассмотрим следующую разность:

$0,1(1+\frac{35}{36}+…+\frac{25}{36})+\frac{12}{36}-(0,1(\frac{12}{36}+\frac{11}{36}…+\frac{1}{36})+\frac{12}{36})=$

$=0,1(1+\frac{35}{36}+…+\frac{25}{36}-(\frac{12}{36}+\frac{11}{36}…+\frac{1}{36}))=$

$=\frac{0,1((36+35+…+24)-(12+11+…+1)}{36}=$

$=\frac{\frac{(36+25)\cdot 12}{2}+\frac{(12+1)\cdot 12}{2}}{360}=$

$=\frac{12(61-13)}{720}=\frac{48}{60}=\frac{4}{5}=0,8.$

Итак, Эльвира выплатит банку в течение первого года кредитования на $800$ тыс. рублей больше, нежели в течение третьего года.

Ответ: $800$.

$log_3(ax^3+a)-2log_3\sqrt{x+1}=log_3x;$

$\begin{cases}\frac{ax^3+a}{x+1}=x,\\x+1>0,\\ax^3+a>0,\\x>0;&\end{cases}$

$\begin{cases}ax^3+a=x^2+x,\\ax^3+a>0,\\x>0;&\end{cases}$

$\begin{cases}a(x+1)(x^2-x+1)=x(x+1),\\a(x+1)(x^2-x+1)>0,\\x>0;&\end{cases}$

$\begin{cases}ax^2-(a+1)x+a=0,\\a>0,\\x>0;&\end{cases}$

Необходимо, чтобы уравнение $ax^2-(a+1)x+1=0$ имело хотя бы один положительный корень при $a>0.$

Рассмотрим функцию $f(x)=ax^2-(a+1)x+a,a>0.$ Пусть $x_v$ – вершина параболы.

На рисунке изображены случаи, когда хотя бы один корень уравнения $f(x)=0$ больше нуля:

Имеем

$\left[\begin{array}{rcl}f(0)<0,\\\begin{cases}D\geq 0,\\x_v>0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}a<0,\\\begin{cases}(a+1)^2-4a^2\geq 0,\\\frac{a+1}{2a}>0;\end{cases}\end{array}\right.$

Первая строка совокупности «отпадает» – мы рассматриваем случай $a>0.$

$\begin{cases}(1-a)(3a+1)\geq 0,\\\frac{a+1}{2a}>0;&\end{cases}$

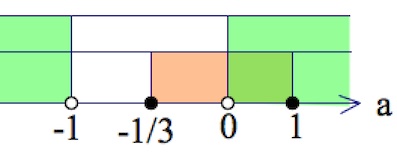
$x\in (0;1].$

Ответ: $(0;1].$