Разбор заданий 13-18 Тренировочной работы
13. Дано уравнение $4^{sinx\cdot tgx}\cdot 2^{\frac{1}{cosx}}=8^{tgx}.$
a) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие интервалу $[2,5\pi; 4\pi].$
Решение: + показать
a)
$4^{sinx\cdot tgx}\cdot 2^{\frac{1}{cosx}}=8^{tgx};$
$2^{2sinx\cdot tgx+\frac{1}{cosx}}=2^{3tgx};$
$2sinx\cdot tgx+\frac{1}{cosx}=3tgx;$
$2sin^2x+1=3sinx,cosx\neq 0;$
$2sin^2x-3sinx+1=0,cosx\neq 0;$
$\begin{cases}\left[\begin{array}{rcl}sinx=1,\\sinx=\frac{1}{2},\end{array}\right.\\cosx\neq 0;\end{cases}$
$sinx=\frac{1}{2};$
$x=\frac{\pi}{6}+2\pi n,$ $x=\frac{5\pi}{6}+2\pi n, n\in Z.$
б) Укажем корни уравнения, принадлежащие интервалу $[2,5\pi; 4\pi].$
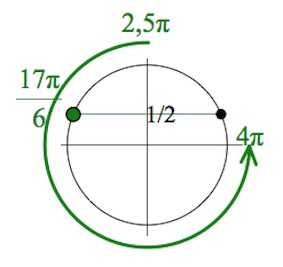
$x=\frac{17\pi}{6}.$
Ответ:
a) $\frac{\pi}{6}+2\pi n,$ $\frac{5\pi}{6}+2\pi n, n\in Z.$
б) $\frac{17\pi}{6}.$
14. Через ребро $BC$ правильной треугольной призмы $ABCA_1B_1C_1$ под углом $60^{\circ}$ к плоскости $ABC$
проведена плоскость $\alpha$. Известно, что площадь сечения призмы плоскостью $\alpha$ равна $14\sqrt3$, а высота призмы равна $3$.
а) Докажите, что плоскость $\alpha$ делит ребро $A_1B_1$ в отношении $1:3$, считая от точки $B_1$.
б) Найдите объем меньшей части, отсекаемой от призмы $ABCA_1B_1C_1$ плоскостью $\alpha$.
Решение: + показать
а) Пусть $M$ – точка, по которой плоскость $\alpha$ пересекает ребро $A_1B_1.$
Так как плоскости оснований призмы параллельны, то плоскость $\alpha$, пересекающая плоскость $ABC$ по прямой $BC$, пересечет плоскость $A_1B_1C_1$ по прямой, параллельной $BC$ (или $B_1C_1$). Проводим через точку $M$ прямую, параллельную $B_1C_1$. Пусть она пересекает ребро $A_1C_1$ в точке $N$.
Тогда трапеция (равнобокая) $MNCB$ – сечение призмы плоскостью $\alpha.$
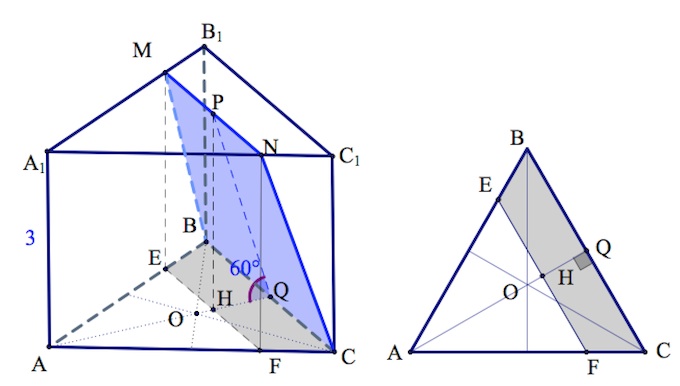
Пусть $E,F$ – проекции точек $M,N$ на плоскость $ABC$ соответственно. Тогда $EFCB$ – проекция $MNCB$ на плоскость $ABC$. И так как $S_{MNCB}=\frac{S_{EFCB}}{cos\alpha}$, где $\alpha =60^{\circ}$ – угол между плоскостями $\alpha $ и $ABC,$ то, согласно условию, $14\sqrt3=\frac{S_{EFCB}}{\frac{1}{2}}.$ Откуда $S_{EFCB}=7\sqrt3.$
Пусть $PQ$ – высота трапеции $MNCB$, причем $P$ – середина $MN.$ Пусть $P$ проецируется в точку $H$. Очевидно, $H$ попадает на медиану (назовем ее $AQ$) к стороне $BC$ треугольника $ABC.$ Медиана $AQ$ перпендикулярна $BC,$ по теореме о трех перпендикулярах и $PQ$ перпендикулярна $BC$, то есть $\angle PQH$ – угол между плоскостями сечения и $ABC.$
Так как $PH=3$, то из треугольника $PQH$ $HQ=\frac{3}{tg60^{\circ}}=\sqrt3.$
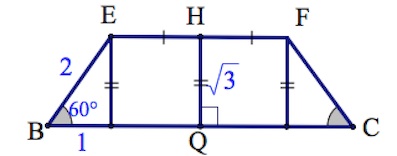
Тогда
$7\sqrt3=\frac{EF+BC}{2}\cdot \sqrt3;$
$7=\frac{EF+(EF+2)}{2};$
$EF=6.$
Итак, $EF=6,BC=8,$ то есть коэффициент подобия треугольников $AEF,ABC$ – есть $\frac{3}{4}$. Откуда $AE:AB=3:4$ или $BE:EA=1:3$. В свою очередь, это означает, что и $MB_1:MA_1=1:3$, то есть плоскость $\alpha$ делит ребро $A_1B_1$ в отношении $1:3$, считая от точки $B_1$.
Что и требовалось доказать.
б) $V_{MB_1C_1NCB}=V_{MB_1C_1NB}+V_{BNCC_1},$ где $MB_1C_1NB$ – пирамида с основанием $MB_1C_1N,$ высотой $BB_1,$ равной $3$ и $BNCC_1$ – пирамида с основанием $BCC_1$. У пирамиды $BNCC_1$ высота равна $\sqrt3$, так как расстояние от точки $N$ до плоскости $BCC_1$ – есть расстояние от точки $F$ до $BCC_1$ (так как $NF\parallel BCC_1$), а в свою очередь расстояние от $F$ до $BCC_1$ – есть расстояние от $H$ до $BCC_1$, так как $HF\parallel BCC_1$. Ну а расстояние от $H$ до $BCC_1$ – есть $HQ$, ведь $HQ$ – перпендикуляр к плоскости $BCC_1$.
$V_{MB_1C_1NCB}=\frac{S_{MB_1C_1N}\cdot BB_1}{3}+\frac{S_{BCC_1}\cdot HQ}{3};$
$V_{MB_1C_1NCB}=\frac{7\sqrt3\cdot 3}{3}+\frac{12\cdot \sqrt3}{3};$
$V_{MB_1C_1NCB}=11\sqrt3.$
При этом $V_{ABCA_1B_1C_1}=\frac{192\sqrt3}{4}.$ Объем многогранника $A_1MNCAB$ тогда равен $\frac{192\sqrt3}{4}-11\sqrt3=\frac{73\sqrt3}{2},$ то есть многогранник $A_1MNCAB$ занимает большую часть призмы.
Итак, объем меньшей части, отсекаемой от призмы $ABCA_1B_1C_1$ плоскостью $\alpha$ – есть $11\sqrt3.$
Ответ: б) $11\sqrt3$.
15. Решите неравенство $\frac{(3^x-3)^3}{2\cdot 3^x-4}\leq \frac{27^x-2\cdot 3^{2x+1}+3^{x+2}}{3^x-9^x+2}.$
Решение: + показать
$\frac{(3^x-3)^3}{2\cdot 3^x-4}\leq \frac{27^x-2\cdot 3^{2x+1}+3^{x+2}}{3^x-9^x+2};$
$\frac{(3^x-3)^3}{2(3^x-2)}\leq \frac{3^{3x}-6\cdot 3^{2x}+9\cdot 3^{x}}{(2-3^x)(3^x+1)};$
$\frac{(3^x-3)^3}{2(3^x-2)}\leq \frac{3^x(3^x-3)^2}{(2-3^x)(3^x+1)};$
$\frac{(3^x-3)^2}{3^x-2}(\frac{3^x-3}{2}+\frac{3^x}{3^x+1})\leq 0;$
$\frac{(3^x-3)^2}{3^x-2}\cdot \frac{(3^x-3)(3^x+1)+2\cdot 3^x}{2(3^x+1)}\leq 0;$
$\frac{(3^x-3)^2}{3^x-2}((3^x-3)(3^x+1)+2\cdot 3^x})\leq 0;$
$\frac{(3^x-3)^2(3^{2x}-3)}{3^x-2}\leq 0;$
$\frac{(3^x-3^1)^2(3^{2x}-3^1)}{3^x-3^{log_32}}\leq 0;$
$\frac{(x-1)^2(2x-1)}{x-log_32}\leq 0;$
Заметим, $\frac{1}{2}=log_3\sqrt3<log_32<log_33=1.$
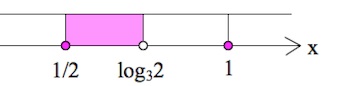
$x\in [\frac{1}{2};log_32)\cup${$1$}.
Ответ: $[\frac{1}{2};log_32)\cup${$1$}.
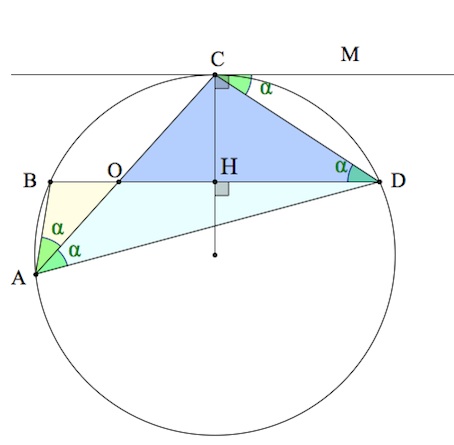
16. В окружности проведены хорды $AC$ и $BD$, пересекающиеся в точке $O$, причем касательная к окружности, проходящая через точку $C$, параллельна $BD$.
а) Докажите, что $DC^2=AC\cdot CO.$
б) Найдите площадь треугольника $CDO$, если известно, что $AB:BO=3:1$, а площадь треугольника $ACD$ равна $36$.
Решение: + показать
а) Пусть $M$ – точка касательной к окружности, проходящей через точку $C$.
Пусть $\angle BAC=\alpha,$ тогда и $\angle CDB=\alpha$ (указанные углы – вписанные, опирающиеся на одну дугу).
Так как касательная к окружности, проходящая через точку $C$, параллельна $BD$, то углы $CDB,CDM$ равны как соответственные. То есть $\angle DCM=\alpha.$ При этом, поскольку угол между касательной и секущей равен половине градусной мере отсекаемой дуги ($CD$), так же, как и $\angle CAD$, то $\angle CAD=\alpha.$
У треугольников $COD,CDA$ угол $C$ – общий.
Итак, треугольники $COD,CDA$ подобны по двум углам.
Тогда $\frac{AC}{DC}=\frac{DC}{CO},$ откуда $DC^2=AC\cdot CO.$
Что и требовалось доказать.
б) Треугольники $AOB,ADC$ подобны ( так как $\Delta DOC$ подобен $\Delta ADC$ из пункта (a) и $\Delta DOC$ подобен $\Delta AOB$ по двум углам).
Тогда $3=\frac{AB}{BO}=\frac{DC}{CO}$.
Но при этом $\frac{DC}{CO}=3$ – коэффициент подобия треугольников $ADC,DOC.$ Тогда площадь треугольника $DOC$ в 9 раз меньше площади треугольника $ADC.$
Итак, площадь треугольника $DOC$ равна $4$.
Ответ: б) $4$.
17. Саша положил некоторую сумму в банк на $4$ года под $10$% годовых. Одновременно с ним Паша такую же сумму положил на два года в другой банк под $15$% годовых. Через два года Паша решил продлить срок вклада еще на $2$ года. Однако к тому времени процентная ставка по вкладам в этом банке изменилась и составляла уже $p$% годовых. В итоге через четыре года на счету у Паши оказалась большая сумма, чем у Саши, причем эта разность составила менее $10$% от суммы, вложенной каждым первоначально. Найдите наибольшее возможное целое значение процентной ставки $p$.
Решение: + показать
Пусть Саша положил сумму $x$ в банк на $4$ года под $10$% годовых. Тогда через $4$ года на его счету – $1,1^4\cdot x$ рублей.
Паша, положив туже сумму $x$ в другой банк под $15$% годовых, через два года на счету будет иметь $1,15^2\cdot x$ рублей.
Паша продлевает срок вклада на $2$ года, но уже с другой процентной ставкой $(p$%).
Тогда в итоге через $4$ года на счету у Паши окажется $(\frac{100+p}{100})^2\cdot 1,15^2\cdot x$ рублей.
Так как разность между суммами на счетах Саши и Паши спустя $4$ года составила менее $10$% от суммы, вложенной каждым первоначально (у Паши – большая сумма), то
$(\frac{100+p}{100})^2\cdot 1,15^2\cdot x-1,1^4\cdot x<0,1x;$
$(\frac{100+p}{100})^2\cdot 1,15^2-1,1^4<0,1;$
$(\frac{100+p}{100})^2<\frac{1,1^4+0,1}{1,15^2};$
$(\frac{100+p}{100})^2<\frac{\frac{121^2+1000}{10000}}{\frac{115^2}{10000}};$
$(\frac{100+p}{100})^2<\frac{15641}{115^2};$
$(\frac{100+p}{100}-\frac{\sqrt{15641}}{115})(\frac{100+p}{100}+\frac{\sqrt{15641}}{115})<0;$
$(p-(\frac{100\sqrt{15641}}{115}-100))(p+\frac{100\sqrt{15641}+100}{115})<0;$
$p-(\frac{100\sqrt{15641}}{115}-100)<0;$
$p\in (0;\frac{20\sqrt{15641}}{23}-100);$
Заметим, что
$125=\sqrt{15625}<\sqrt{15641};$
Тогда
$8\frac{16}{23}<\frac{20\sqrt{15641}-2300}{23}.$
При этом $\frac{20\sqrt{15641}-2300}{23}<9$, в чем несложно убедиться:
$\frac{20\sqrt{15641}-2300}{23}\vee 9;$
$20\sqrt{15641}-2300\vee 207;$
$20\sqrt{15641}\vee 2507;$
$6256400<6285049.$
Итак, максимальное целое значение $p$ из $(0;\frac{20\sqrt{15641}}{23}-100)$ – это $8.$
Ответ: $8$.
18. Для каждого $a$ определите наибольшее значение функции $f(x)=x^3-3ax^2$ на отрезке $[-2; 2]$.
Решение: + показать
$f(x)=x^2(x-3a).$
График проходит через точки $(0;0),(3a;0),$ причем $(0;0)$ – корень четной кратности.
Так как $f'(x)=3x^2-6ax,$ то точки экстремума функции – $0$ и $2a.$
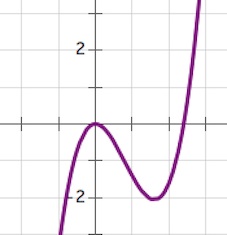
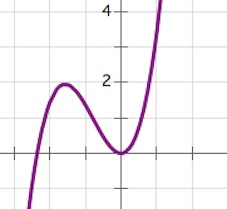
Наибольшее значение функции $f(x)$ на отрезке $[-2; 2]$ – максимум из $f(-2);f(2);f(0);f(2a)}$ при условии, что $2a\in [-2;2]$. Если же $2a$ не входит в $[-2;2]$, то наибольшее значение функции на отрезке $[-2; 2]$ – максимум из $f(-2);f(2);f(0)}$.
$f(0)=0;$
$f(2)=8-12a;$
$f(-2)=-8-12a;$
$f(2a)=-4a^3;$
Очевидно, $8-12a>-8-12a$ при любом $a$. Поэтому на наибольшее значение функции на отрезке $[-2; 2]$ значение $f(-2)$ претендовать не может.
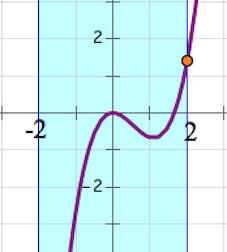
1) Замечаем, что если $a>0$, то наибольшее значение $f(x)$ на отрезке $[-2; 2]$ достигается в $x=2$ или в $x=0.$
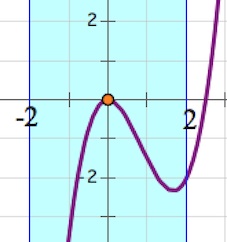
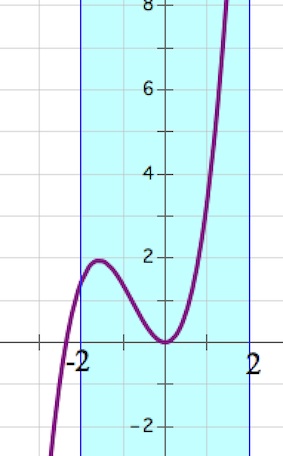
2) Если $a<0$, то наибольшее значение $f(x)$ на отрезке $[-2; 2]$ достигается в $x=2a$ или в $x=2$. Причем, если $2a$ не входит в отрезок $[-2; 2]$, то $f(2a)$ на наибольшее значение претендовать не будет.
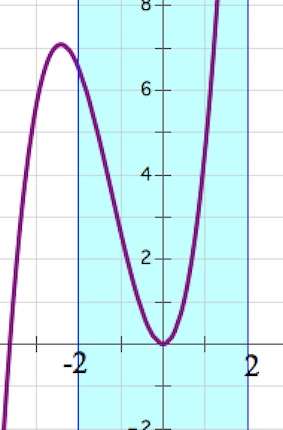
3) Если $a=0$, то наибольшее значение достигается в $x=2.$
Рассмотрим детально случай 1 ($a>0$).
При $a>0$ следует выбрать большее из $f(2),f(0).$
$f(0)=0$, $f(2)=8-12a.$
Если $0<8-12a$ (с учетом $a>0$ имеем: $0<a<\frac{2}{3}$), то наибольшее значение функции – это $8-12a.$
Если $8-12a\leq 0$ (с учетом $a>0$ имеем: $a\geq \frac{2}{3}$), то наибольшее значение функции – это $0.$
Рассмотрим детально случай 2 ($a<0$).
a) При $a<0$ следует выбрать большее из $f(2),f(2a)$, если $2a\in [-2;2]$.
Итак, $a\in [-1;0).$
Наибольшим значением $f(x)$ на указанном отрезке будет $f(2)$, то есть $8-12a,$ если
$8-12a>-4a^3$ при $a\in [-1;0);$
$a^3-3a+2>0$ при $a\in [-1;0);$
$(a-1)^2(a+2)>0$ при $a\in [-1;0);$
А это так.
Наибольшим значением $f(x)$ на указанном отрезке не может оказаться $f(2a)$, так как если
$8-12a<-4a^3$,
то
$a\in (-\infty;-2)$,
а у нас $a\in [-1;0).$
б) Если же $2a$ не входит в $[-2;2]$ (то есть $a\in (-\infty;-1)$), то наибольшее значение функции на указанном отрезке – $8-12a.$
Итак, резюмируя вышесказанное, получаем:
при $a\in (-\infty;\frac{2}{3})$ наибольшее значение $f(x)$ на $[-2; 2]$ – есть $8-12a;$
при $a\in [\frac{2}{3};+\infty)$ наибольшее значение $f(x)$ на $[-2; 2]$ – есть $0.$
Ответ:
$a\in (-\infty;\frac{2}{3})$: $8-12a;$
$a\in [\frac{2}{3};+\infty)$: $0.$













Как x будет равен 5pi/6, если sinX = 1? Частный случай же?
5pi/6 выскочил из уравнения sinx=0,5.
А уравнение sinx=1 «уничтожено» условием cosx≠0
Спасибо вам большое за такой сайт! :)
Виталий, заходите, рада)
В задании № 15 в ответе ошибка : Левая точка должна быть 1/2, а у Вас -1/2? Или я ошибаюсь?
Людмила, спасибо! В решении нет ошибок. Это в ответ закралась опечатка – влез минус..
Исправлено.
Все сижу, не могу понять, почему в 15 задании меняется знак, не могли бы вы объяснить?
Гюля, потому что была опечатка – знак повернулся не так))
Спасибо!
В 15 задании,4 строка после “спрятать”, числитель последней дроби,вроде должно быть 3 в степени х.
Слава, конечно. Спасибо!