Профильный уровень
Разбор заданий 1-12. Часть С (задания 13-19) смотрим здесь
1. Установка счётчиков холодной и горячей воды стоит 2300 рублей. До установки счётчиков за водоснабжение платили 1200 рублей ежемесячно. После установки счётчиков ежемесячная оплата стала 600 рублей. Через сколько месяцев экономия впервые превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
Решение: + показать
Пусть через $n$ месяцев экономия впервые превысит затраты на установку счётчиков. Тогда
$2300+600n< 1200n;$
$600n> 2300;$
$6n> 23;$
$n> 3\frac{5}{6}.$
Наименьшее натуральное значение $n,$ отвечающее неравенству – это $4.$
Через $4$ месяца экономия впервые превысит затраты на установку счётчиков.
Ответ: $4.$
2. На диаграмме показано количество выплавляемой меди в 10 странах мира в 2006 году. По горизонтали указываются страны, по вертикали – количество выплавляемой меди (в тысячах тонн). Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимает Польша?
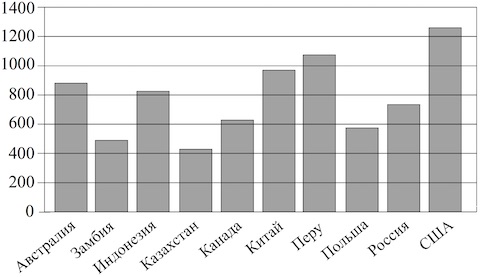
Решение: + показать
Польша занимает $8$-е место.
Ответ: $8.$
3. Найдите площадь многоугольника по данным рисунка.

Решение: + показать

По теореме Пифагора найдем неизвестную сторону $AD$ прямоугольника:
$AD^2=13^2-5^2;$
$AD^2=144.$
Откуда $AD=12.$
Стало быть, $S=AB\cdot AD=5\cdot 12=60.$
Ответ: $60.$
4. Чтобы выйти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение: + показать
Команде удастся выйти в следующий круг соревнований, если она
выиграет в первой игре и выиграет во второй игре (вероятность – $0,4\cdot 0,4$)
или
выиграет первую игру и сыграет вничью во второй игре ($0,4\cdot 0,2$)
или
сыграет вничью в первой игре и выиграет во второй игре ($0,2\cdot 0,4$).
Итак, искомая вероятность – $0,4\cdot 0,4+0,4\cdot 0,2+0,2\cdot 0,4=0,32.$
Ответ: $0,32.$
5. Найдите корень уравнения $\sqrt{52-6x}=4.$
Решение: + показать
$\sqrt{52-6x}=4;$
$52-6x=16;$
$6x=36;$
$x=6.$
Ответ: $6.$
6. Найдите площадь прямоугольника, диагональ которого равна $13,$ а одна из сторон равна $5.$
Решение: + показать

По теореме Пифагора найдем неизвестную сторону $AD$ прямоугольника:
$AD^2=13^2-5^2;$
$AD^2=144.$
Откуда $AD=12.$
Стало быть, $S=AB\cdot AD=5\cdot 12=60.$
Ответ: $60.$
7. На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-5;8).$ Найдите наибольшее значение функции на отрезке $[-2;3].$

Решение: + показать

Ответ: $3.$
8. Дана правильная четырёхугольная призма $ABCDA_1B_1C_1D_1$, площадь основания которой равна $6$, а боковое ребро равно $7$. Найдите объём многогранника, вершинами которого являются точки $A,B,C,A_1,B_1.$

Решение: + показать
Многогранник, вершинами которого являются точки $A,B,C,A_1,B_1$ – пирамида с основанием $ABB_1A_1$ вершиной $C.$

Поэтому $V=\frac{S_{ABB_1A_1}\cdot H}{3},$ где $H$ – высота пирамиды.
Причем, в силу того, что данная четырехугольная призма правильная, – $CB\perp (ABB_1A_1),$ то есть $H=CB.$
Также очевидно, что $ABB_1A_1$ – прямоугольник.
Итак, $V=\frac{AA_1\cdot AB\cdot CB}{3}=\frac{AA_1\cdot (AB\cdot CB)}{3}=\frac{7\cdot 6}{3}=14.$
Ответ: $14.$
9. Найдите $tg\alpha,$ если $sin\alpha =-\frac{7}{\sqrt{149}}$ и $\alpha \in (\frac{3\pi}{2};2\pi).$
Решение: + показать
$sin^2\alpha+cos^2\alpha=1;$
$(-\frac{7}{\sqrt{149}})^2+cos^2\alpha=1;$
$\frac{49}{149}+cos^2\alpha=1;$
$cos^2\alpha=1-\frac{49}{149};$
$cos^2\alpha=\frac{100}{149};$
$cos\alpha =\pm \frac{10}{\sqrt{149}};$
Так как $\alpha \in (\frac{3\pi}{2};2\pi),$ то $cos\alpha =\frac{10}{\sqrt{149}}.$
Тогда $tg\alpha =\large\frac{sin \alpha}{cos \alpha}=\frac{-\frac{7}{\sqrt{149}}}{\frac{10}{\sqrt{149}}}=-0,7.$
Ответ: $-0,7.$
10. При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала $f_0=160$ Гц и равна: $f=f_0\cdot \frac{c+u}{c-v}$ (Гц), где $c$ — скорость распространения сигнала в среде (в м/с), а $u=8$ м/с и $v=16$ м/с — скорости приёмника и источника относительно среды соответственно. При какой скорости $c$ (в м/с) распространения сигнала в среде частота $f$ сигнала в приёмнике будет равна $170$ Гц?
Решение: + показать
Так как частота $f$ сигнала в приёмнике равна $170$ Гц, то $170=f_0\cdot \frac{c+u}{c-v}.$
Подставляем известные значения $f_0,u,v.$ Получаем:
$170=160\cdot \frac{c+8}{c-16};$
$17(c-16)=16(c+8);$
$17c-17\cdot 16=16c+16\cdot 8;$
$c=16(8+17);$
$c=400.$
Ответ: $400.$
11. Завод получил заказ на партию штампованных деталей. Один автомат может отштамповать все детали за 16 часов. Через 2 часа после того, как первый автомат начал штамповать детали, начал работу второй такой же автомат, и оставшиеся детали были распределены между двумя автоматами поровну. Сколько всего часов потребовалось на выполнение этого заказа?
Решение: + показать
Пусть требуется отштамповать $n$ деталей. Так как один автомат может отштамповать все детали за $16$ часов, то скорость его работы – $\frac{n}{16}$. Автоматы одинаковые, скорость работы второго – также $\frac{n}{16}.$
За два часа первый автомат отштампует $2\cdot \frac{n}{16}$ (или $\frac{n}{8}$) деталей. Останется отштамповать $\frac{7n}{8}$ деталей.
Далее оставшиеся детали были распределены между двумя автоматами поровну, значит каждый автомат отштамповал в дальнейшем по $\frac{7n}{16}$ деталей, на что ушло $\frac{\frac{7n}{16}}{\frac{n}{16}},$ то есть $7$ часов.
Итак, на выполнение всего заказа потребовалось $2+7,$ то есть $9$ часов.
Ответ: $9.$
12. Найдите точку минимума функции $y=\sqrt{x^2-6x+11}.$
Решение: + показать
Точка минимума функции $f(x)=x^2-6x+11$ – это $3.$ Действительно, график $f(x)$ – парабола с ветвями вверх, абсцисса вершины – $\frac{6}{2}=3.$
Внешняя функция $y=\sqrt{f}$ – возрастающая, а значит данная функция сохраняет характер монотонности внутренней функции $f(x)$ на области определения (на $R$).
Итак, $x=3$ – точка минимума не только $f(x),$ но и точка минимума функции $y=\sqrt{x^2-6x+11}.$
Ответ: $3.$
Номера 13-19 далее









Спасибо вам. Проверила свои знания.
:)
А где можно посмотреть вариант 10 из этой же диагностики?
А задачи 3 и 6 действительно одинаковые?
Действительно! Но так и есть)))