Разбор заданий части В Т/Р по математике от 28.01.14
В1. В доме, в котором живет Женя, один подъезд. На каждом этаже по восемь квартир. Женя живет в квартире 87. На каком этаже живет Женя?
Решение:+ показать
Женя живет на 11 этаже, так как $87:8=10\frac{7}{8}$.
Ответ: 11.
В2. Для приготовления вишневого варенья на 1 кг вишни нужно 1,5 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 16 кг вишни?
Решение: + показать
При приготовлении варенья на 16 кг вишни расходуется $16\cdot 1,5=24$ кг сахара. Следовательно, требуется купить 24 упаковки (килограммовых) сахара.
Ответ: 24.
В3. На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место занимала Папуа – Новая Гвинея, одиннадцатое место – Индия. Какое место занимал Узбекистан?
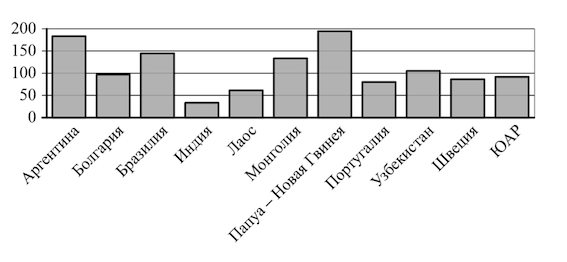
Решение: + показать
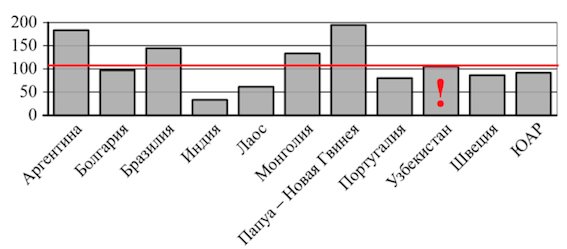
Ответ: 5.
В4. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.

Определите, в каком из салонов покупка обойдётся дороже всего (с учётом переплаты), и в ответ напишите эту наибольшую сумму в рублях.
Решение: + показать
Эпсилон:
Первоначальный взнос: $21600\cdot 0,2=4320$ + за 6 месяцев сам кредит $3600\cdot 6=21600$. Итого $4320+21600=25920$ (рублей).
Дельта:
Первоначальный взнос: $22300\cdot 0,15=3345$ + за 12 месяцев сам кредит $1860\cdot 12=22300$. Итого $3345+22300=25665$ (рублей).
Омикрон:
Первоначальный взнос: $24000\cdot 0,2=4800$ + за 12 месяцев сам кредит $1750\cdot 12=21000$. Итого $4800+21000=25800$ (рублей).
В салоне «Эпсилон» покупка обойдётся дороже всего (с учётом переплаты) и составит $25920$ рублей.
Ответ: 25920.
В5. Точки $D$, $E$, $F$ – середины сторон треугольника $ABC$. Периметр треугольника $DEF$ равен 5. Найдите периметр треугольника $ABC$.
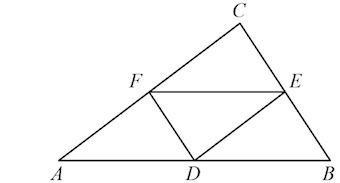
Решение: + показать
Так как $E$ и $F$ – середины сторон $AC,\;BC$ соответственно, то $FE$ – средняя линия треугольника $ABC$.
Следовательно, по свойству средней линии $AB=2EF.$
Аналогично $BC=2FD,\;AC=2DE.$
А так как по условию периметр $DEF$ равен 5, то $EF+FD+DE=5.$
Но тогда
$P_{ABC}=AB+BC+AC=2EF+2FD+2DE=2(EF+FD+DE)=$
$=2\cdot 5=10.$
Ответ: 10.
В6. В сборнике билетов по математике всего 20 билетов, в 5 из них встречается вопрос по теории вероятностей. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей.
Решение: + показать
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей есть $\frac{5}{20}=\frac{1}{4}=0,25.$
Ответ: 0,25.
В7. Найдите корень уравнения $\frac{1}{9x+2}=\frac{1}{8x-4}.$
Решение: + показать
$\frac{1}{9x+2}=\frac{1}{8x-4};$
$9x+2=8x-4;$
$x=-6.$
Ответ: -6.
В8. Два угла вписанного в окружность четырёхугольника равны 125° и 47°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
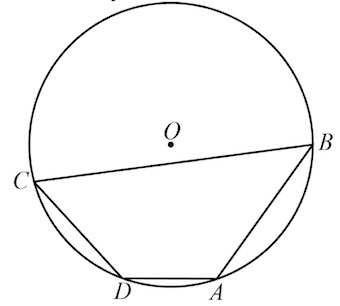
Решение: + показать
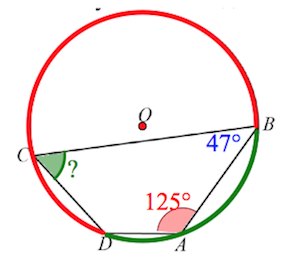 Пусть, например*, $\angle A=125^{\circ}$ и $\angle B=47^{\circ}.$
Пусть, например*, $\angle A=125^{\circ}$ и $\angle B=47^{\circ}.$
Вписанный угол $A$ опирается на дугу $BCD$, а угол $C$ – на дугу $BAD$. Эти две дуги образуют собой окружность, то есть сумма градусных мер указанных дуг – 360˚. Тогда сумма вписанных углов $A$ и $C$, опирающихся на эти дуги, будет равна 180˚, ведь вписанный угол измеряется половиной градусной меры дуги, на которую опирается.
Тогда $\angle C=180^{\circ}-\angle A=180^{\circ}-125^{\circ}=55^{\circ}.$
Аналогично $\angle D=180^{\circ}-\angle B=180^{\circ}-47^{\circ}=133^{\circ}.$
Меньший из найденных углов – угол $C$, градусная мера которого 55˚.
* Заметим, данные два угла не могут быть противоположными (по вышесказанному), иначе их сумма должна была бы равняться 180°.
Ответ: 55.
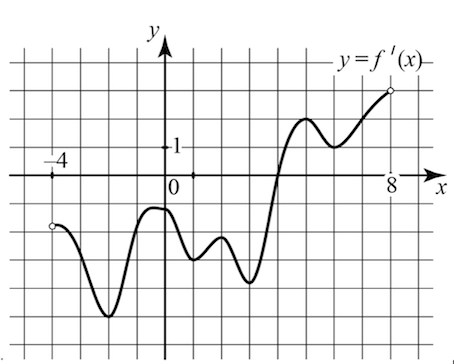
В9. На рисунке изображён график производной y = f ′(x) функции f (x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция f (x) принимает наименьшее значение?
Решение: + показать
На отрезке [−3; 1] $y=f'(x)$ принимает отрицательные значения (лежит ниже оси $ox$), значит на отрезке [−3; 1] функция $f(x)$ убывает. 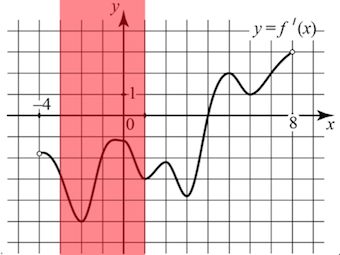
Соответственно, наименьшее значение функции $f(x)$ на отрезке [−3; 1] будет достигаться на правом конце отрезка, то есть в точке 1.
Ответ: 1.
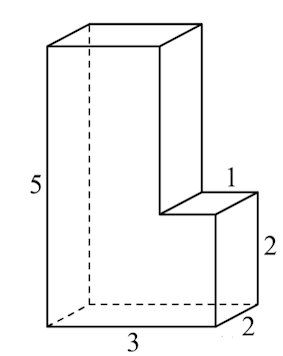
В10. Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).
Решение: + показать
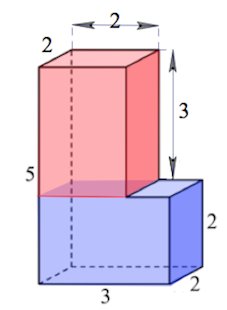
Многогранник, изображенный на рисунке, можно разбить, например, на 2 прямоугольных параллелепипеда так, как это показано на рисунке.
Причем, объемы $V_1,\;V_2$ у этих прямоугольных параллелепипедов равны: $V_1=V_2=2\cdot 2\cdot 3=12$ (Объем прямоугольного параллелепипеда есть произведение трех его измерений (длины, ширины и высоты)).
Тогда искомый объем есть $2\cdot 12=24.$
Ответ: 24.
В11. Найдите значение выражения $-\frac{22}{cos^234^{\circ}+cos^2124^{\circ}}.$
Решение: + показать
Ко второму слагаемому знаменателя применяем формулу приведения:
$-\frac{22}{cos^234^{\circ}+cos^2124^{\circ}}=-\frac{22}{cos^234^{\circ}+cos^2(90^{\circ}+34^{\circ})}=$
$=-\frac{22}{cos^234^{\circ}+sin^234^{\circ}}=-\frac{22}{1}=-22.$
Ответ: -22.
В12. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением $pV^{1,4}=const$ , где $p$ (атм) — давление в газе, $V$ — объём газа в литрах. Изначально объём газа равен 24 л, а его давление равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде поднялось до 128 атмосфер? Ответ выразите в литрах.
Решение: + показать
Так как изначально объём газа равен 24 л, а его давление равно одной атмосфере, то $1\cdot 24^{1,4}=const.$
Тогда $p=\frac{const}{V^{1,4}}=\frac{24^{1,4}}{V^{1,4}}.$
При давление в сосуде в 128 атмосфер имеем:
$128=\frac{24^{1,4}}{V^{1,4}};$
$2^7=(\frac{24}{V})^{\frac{7}{5}};$
$2^7=((\frac{24}{V})^{\frac{1}{5}})^7;$
Тогда
$2=(\frac{24}{V})^{\frac{1}{5}};$
Возведем обе части равенства в 5-ю степень:
$2^5=\frac{24}{V};$
$32=\frac{24}{V};$
$V=\frac{24}{32};$
$V=0,75.$
Ответ: 0,75.
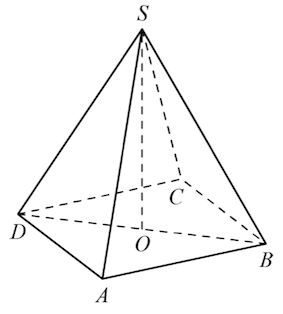
В13. В правильной четырехугольной пирамиде $SABCD$ точка $O$ – центр основания, $S$ – вершина, $SA=10,\;BD=16.$ Найдите длину отрезка $SO.$
Решение: + показать
Уточним, раз пирамида $SABCD$ правильная, то в основании лежит квадрат и вершина проецируется в центр этого квадрата, то есть в точку пересечения диагоналей.
В частности, у правильной пирамиды все боковые ребра равны между собой ($SA=SB=SC=SD$).
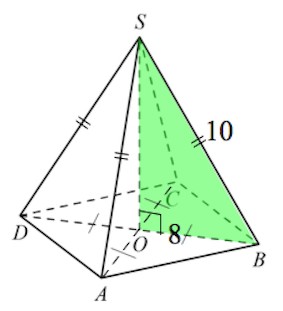
Рассмотрим, например, треугольник $SOB$. Он прямоугольный, так как $SO\perp (ABCD)$, а значит $SO$ перпендикулярна любой прямой плоскости $(ABCD)$, в частности, прямой $BD$.
В нем $SB=10$ и $BO=8$ (так как диагонали в квадрате равны и точкой пересечения делятся пополам).
По т. Пифагора $SO=\sqrt{10^2-8^2}=6.$
Ответ: 6.
В14. Первый и второй насосы наполняют бассейн за 10 минут, второй и третий – за 15 минут, а первый и третий – за 24 минуты. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение: + показать
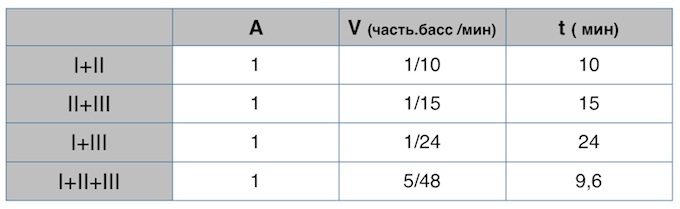
Как именно заполнялась таблица?
Принимаем работу (она состоит в наполнении бассейна) за 1.
I и II трубы наполняют бассейн за 10 минут, значит их совместная скорость заполнения бассейна $\frac{1}{10}$ часть бассейна в минуту.
Аналогично II и III трубы заполняют бассейн со скоростью $\frac{1}{15}$ часть бассейна в минуту.
И скорость заполнения бассейна I и III трубами – $\frac{1}{24}.$
Складывая совместные скорости труб I, II; I, III и II, III, мы получаем удвоенную совместную скорость работы труб I, II и III.
Поэтому совместная скорость заполнения трубами I, II и III бассейна есть $(\frac{1}{10}+\frac{1}{15}+\frac{1}{24}):2=\frac{5}{48}.$
Тогда время заполнения бассейна тремя трубами есть $\frac{1}{\frac{5}{48}}=9,6$ (мин).
Ответ: 9,6.
В15. Найдите точку максимума функции $y=-\frac{x^2+49}{x}.$
Решение: + показать
Найдем производную данной функции, пользуясь правилом дифференцирования частного двух функций:
$\color{red}(\frac{u}{v})’=\frac{u’v-uv’}{v^2}$
$y’=-\frac{2x\cdot x-(x^2+49)\cdot 1}{x^2}=-\frac{x^2-49}{x^2}=\frac{49-x^2}{x^2}=$
$=\frac{(7-x)(7+x)}{x^2}.$
Рассмотрим знаки производной функции на образовавшихся промежутках, а также укажем поведение функции.
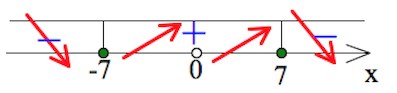
Видим, что $x=7$ – точка максимума.
Ответ: 7.
———————————————————————————————————
Смотрите также задания C1, С2, С3, С4 Тренировочной работы от 28 января 2014 года.
Здесь найдете все варианты работы (с ответами, критериями).










 Пусть, например
Пусть, например




Никак не пойму как делать В14..какой там общий знаменатель.. Найти не могу..:с
10=2*5
15=3*5
24=2*2*2*3
Поэтому общий знаменатель – 2*2*2*3*5. Из этого «набора» мы можем составить и «набор» 2*5, и 3*5, и 2*2*2*3.