Разбор заданий 13-18 Тренировочной работы
13. Дано уравнение $\sqrt{sinx+3}=-2sinx.$
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку $[0;2\pi].$
Решение: + показать
a)
$\sqrt{sinx+3}=-2sinx;$
$sinx+3=4sin^2x,sinx\leq 0;$
$4sin^2x-sinx-3=0, sinx\leq 0;$
$sinx=\frac{1\pm 7}{8}, sinx\leq 0;$
$sinx=-\frac{3}{4};$
$x=-arcsin\frac{3}{4}+2\pi n,$ $x=\pi +arcsin\frac{3}{4}+2\pi n, n\in Z;$
б) Отбор корней уравнения, принадлежащих отрезку $[0;2\pi]:$
$arcsin\frac{3}{4}+\pi$, $2\pi -arcsin\frac{3}{4}$
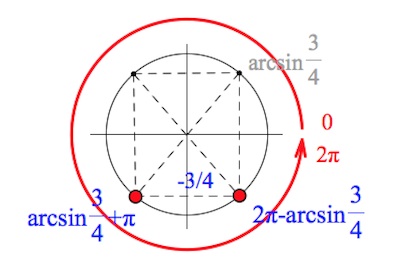
Ответ:
a) $-arcsin\frac{3}{4}+2\pi n,$ $\pi +arcsin\frac{3}{4}+2\pi n, n\in Z;$
б) $arcsin\frac{3}{4}+\pi$, $2\pi -arcsin\frac{3}{4}$.
14. В правильной треугольной пирамиде $PABC$ боковое ребро равно 10, а сторона основания равна $2\sqrt{30}$. Через точки $B$ и $C$ перпендикулярно ребру $PA$ проведена плоскость α.
а) Докажите, что плоскость α делит пирамиду $PABC$ на два многогранника, объемы которых относятся как $2:3$.
б) Найдите площадь сечения пирамиды $PABC$ плоскостью α.
Решение: + показать
a) Построим плоскость α.
Строим в плоскости $ACP$ перпендикуляр $CK$ к $AP$.
В силу того, что пирамида правильная, $KB$ также окажется перпендикуляром к $AP$.
То есть прямая $AP$ перпендикулярна двум пересекающимся прямым плоскости $BCK$, а значит, по признаку перпендикулярности прямой и плоскости, перпендикулярна самой плоскости $BCK$. Плоскость $BCK$ и есть плоскость α.
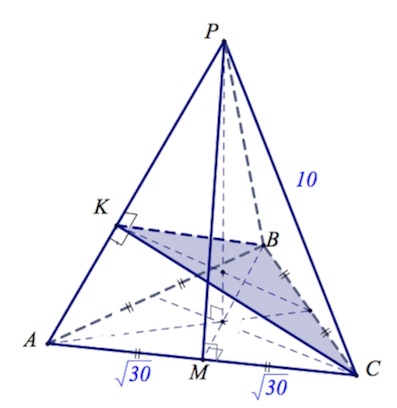
Так как пирамиды $ABCP,ABCK$ имеют одинаковые основания и $AP\perp BKC$, то $\frac{V_{ABCK}}{V_{BCKP}}=\frac{AK}{KP}.$
Найдем $AK$.
Для равнобедренного треугольника $APC$ распишем площадь двумя способами:
$S_{APC}=\frac{AC\cdot PM}{2}=\frac{AP\cdot KC}{2}$
(где $PM\perp AC$).
Откуда
$AC\cdot PM=AP\cdot KC;$
$KC=\frac{AC\cdot PM}{AP}=\frac{AC\cdot \sqrt{AP^2-AM^2}}{AP}=\frac{2\sqrt{30}\cdot \sqrt{70}}{10}=2\sqrt{21}.$
Тогда
$AK=\sqrt{AC^2-KC^2}=\sqrt{(2\sqrt{30})^2-(2\sqrt{21})^2}=6.$
Итак, $\frac{V_{ABCK}}{V_{BCKP}}=\frac{AK}{KP}=6:4=3:2.$
Что и требовалось доказать.
б) Найдем площадь треугольника $BCK$ по формуле Герона:
$S_{BCK}=\sqrt{p(p-BC)(p-BK)(p-CK)},$
где $p=\frac{BC+BK+CK}{2}=\sqrt{30}+2\sqrt{21}.$
Имеем
$S_{BCK}=\sqrt{(\sqrt{30}+2\sqrt{21})(2\sqrt{21}-\sqrt{30})(\sqrt{30})^2}=\sqrt{54\cdot 30}=18\sqrt{5}.$
Ответ: б) $18\sqrt5.$
15. Решите неравенство $\frac{2\sqrt{x+3}}{x+1}\leq \frac{3\sqrt{x+3}}{x+2}$.
Решение: + показать
$\frac{2\sqrt{x+3}}{x+1}\leq \frac{3\sqrt{x+3}}{x+2};$
$\sqrt{x+3}\cdot (\frac{2}{x+1}-\frac{3}{x+2})\leq 0;$
$\sqrt{x+3}\cdot \frac{2x+4-3x-3}{(x+1)(x+2)}\leq 0;$
$\frac{\sqrt{x+3}(1-x)}{(x+1)(x+2)}\leq 0;$
К первому множителю неравенства применяем метод замены множителей
(заменяем разность $\sqrt{x+3}-\sqrt0$ на разность $x+3-0$ при условии $x\geq -3$):
$\frac{(x+3)(1-x)}{(x+1)(x+2)}\leq 0, x\geq -3;$
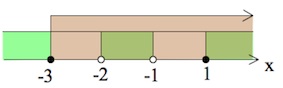
$x\in${$-3$}$\cup (-2;-1)\cup [1;+\infty).$
Ответ: {$-3$}$\cup (-2;-1)\cup [1;+\infty).$
16. В прямоугольном треугольнике $ABC$ синус угла $A$ равен $\frac{1}{3}$. На гипотенузе $AB$ взята точка $H$, а на катете $AC$ – точка $K$. Известно, что прямая $KH$ перпендикулярна гипотенузе и делит треугольник $ABC$ на две равновеликие части.
а) Докажите, что в четырехугольник $KHBC$ можно вписать окружность.
б) Найдите радиус этой окружности, если известно, что $KH=1$.
Решение: + показать
а) В четырехугольник можно вписать окружность, если суммы длин противоположных сторон равны.
Докажем, что $CK+BH=BC+HK.$
Обозначим $BC=x, HK=y$.
Тогда, так как $sinA=\frac{1}{3},$ то $AB=3x,AK=3y.$
Несложно заметить, что, по т. Пифагора, $AC=2\sqrt2x,AH=2\sqrt2y.$
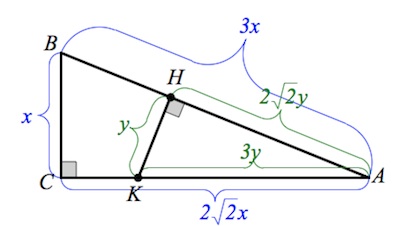
Так как по условию $S_{AHK}=S_{KHBC}$, то есть $2S_{AHK}=S_{ABC}$, то
$2\sqrt2y^2=\frac{2\sqrt2x^2}{2};$
$x=\sqrt2y.$
Итак,
$BC+HK=x+y=\sqrt2y+y.$
И
$CK+BH=(2\sqrt2x-3y)+(3x-2\sqrt2y)=(4y-3y)+(3\sqrt2y-2\sqrt2y)=$
$=y+\sqrt2y.$
Таким образом, мы доказали, что $CK+BH=BC+HK$, то есть в четырехугольник $KHBC$ можно вписать окружность.
б) Пусть радиус окружности, вписанной в $KHBC$, – $r.$
Тогда $r=\frac{S_{KHBC}}{p},$ где $p$ – полупериметр.
Итак,
$r=\large\frac{\frac{S_{ABC}}{2}}{\frac{CK+BH+BC+HK}{2}}=\frac{\frac{\sqrt2x^2}{2}}{\sqrt2y+y}=\frac{\sqrt2y^2}{y(\sqrt2+1)}=$
$=\large\frac{\sqrt2y}{\sqrt2+1}=\normalsize y(2-\sqrt2).$
При $y=1$ получаем, что $r=2-\sqrt2.$
Ответ: б) $2-\sqrt2.$
17. Несколько человек должны были принять участие в экскурсии. Однако двое не смогли в ней участвовать, поэтому остальным экскурсантам пришлось уплатить на 30 руб. больше, чем планировалось (все участники должны были заплатить поровну). Сколько должен был заплатить каждый экскурсант первоначально, если известно, что стоимость экскурсии больше 700 руб., но не более 750 руб.?
Решение: + показать
Пусть каждый из $n$ экскурсантов должен был заплатить первоначально по $x$ рублей. Стоимость экскурсии составляет $xn$ рублей.
На экскурсию отправилось $n-2$ человек, поэтому каждый из них заплатил по $x+30$ рублей. Стоимость экскурсии составляет $(n-2)(x+30)$ рублей.
Имеем
$xn=(n-2)(x+30);$
$30n-2x-60=0;$
$x=15n-30;$
Поскольку по условию стоимость экскурсии больше 700 руб., но не более 750 руб., то
$700<xn\leq 750;$
$700<15n^2-30n\leq 750;$
$\begin{cases}15n^2-30n>700,\\15n^2-30n\leq 750;&\end{cases}$
$\begin{cases}3n^2-6n-140>0,\\n^2-2n-50\leq 0;&\end{cases}$
$\begin{cases}(n-\frac{3+\sqrt{429}}{3})(n-\frac{3-\sqrt{429}}{3})>0,\\(n-(1+\sqrt{51}))(n-(1-\sqrt{51}))\leq 0;&\end{cases}$
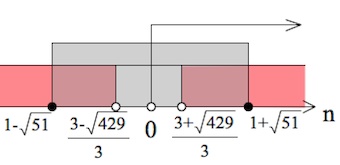
$n\in (\frac{3+\sqrt{429}}{3};1+\sqrt{51}].$
Нас интересуют натуральные значения $n.$
Заметим, $\frac{3+\sqrt{429}}{3}<8<1+\sqrt{51}.$
Действительно, $3+\sqrt{429}<24<3+3\sqrt{51};$
$\sqrt{429}<21<3\sqrt{51};$
$\sqrt{429}<21<\sqrt{459};$
$\sqrt{429}<\sqrt{441}<\sqrt{459};$
При этом числа $\frac{3+\sqrt{429}}{3}$ и $1+\sqrt{51}$ больше 7 и меньше 9 соответственно, в чем несложно убедиться.
Итак, на роль $n$ подходит только число $8.$
Тогда, поскольку $x=15n-30$, то каждый экскурсант первоначально должен был заплатить $15\cdot 8-30$, то есть $90$ рублей.
Ответ: $90$.
18. Найдите все значения $a$, при каждом из которых уравнение
$x^2-acos\frac{\pi x}{2}+a^2-6=0$
имеет ровно один корень.
Решение: + показать
Рассмотрим функцию $f(x)=x^2-acos\frac{\pi x}{2}+a^2-6$.
Она четная, поэтому вместе с каждым корнем $x_0$ уравнение $f(x)=0$ будет иметь и корень $-x_0$. Единственный корень будет в случае $x_0=-x_0=0.$
Если $x=0$, то $-a+a^2-6=0.$ Итак, допустимые значения параметра таковы: $a=-2$ или $a=3.$
Посмотрим, будут ли найденные значения $a$ достаточными для нашего случая.
Если $a=3$, то
$x^2-3cos\frac{\pi x }{2}+9-6=0;$
$x^2+3=3cos\frac{\pi x }{2};$
Минимальное значение, равное 3, левая часть последнего равенства принимает только при $x=0$. При этом максимальное значение правой части также равно $3$ (и при $x=0$ в том числе). Видно, что $x=0$ – единственный корень данного уравнения.
Если $a=-2$, то
$x^2+2cos\frac{\pi x }{2}+4-6=0;$
$x^2-2=-2cos\frac{\pi x }{2};$
Хорошо видно, что помимо $x=0$ корнями уравнения являются и значения $x=\pm 2$, что нас не устраивает.
Ответ: $3.$







Задание 14. У пирамид РСВК и АСВК общее основание СВК, высоты – РК и АК соответственно. Объемы этих пирамид относятся как высоты (общее основание), то есть 6:4=3:2. Можно и такой вариант рассмотреть.
Елена, спасибо за Ваше решение.
Елена, спасибо за ваш вариант!
Здравствуйте. в задании 13 можно ли в ОДЗ писать sinx<0,получается что корень не может быть равен нулю
Мария, да, можно.
Добрый день(или ночь), подскажите, пожалуйста, как в 17 задании из “корень_из(2)/(1 + корень_из(2))” получилось “2 – корень_из(2)”?
буду очень благодарен
Владимир, не пойму вопроса(((