Тренировочный вариант №138 А. Ларина

a)

$2015^x+2016\cdot 2015^{1-x}-4031=0;$

Умножим обе части равенства на $2015^x:$

$2015^{2x}+2016\cdot 2015-4031\cdot 2015^x=0;$

$(2015^{x})^2-4031\cdot 2015^x+2016\cdot 2015=0;$

Заметим, $2016+2015=4031$.

По теореме Виета

$2015^x=2015$ или $2015^x=2016.$

Откуда $x=1$ или  $x=log_{2015}2016.$

б) Произведем отбор корней уравнения из$[log_{2017}2016;log_{2016}2017].$

1) Так как

$log_{2017}2016<log_{2017}2017=1$

и

$log_{2016}2017>log_{2016}2016=1$,

то

$1\in [log_{2017}2016;log_{2016}2017].$

2) Сравним $log_{2016}2017$ и $log_{2015}2016.$

$\frac{log_{2016}2017}{log_{2015}2016}=log_{2016}2017\cdot log_{2016}2015.$

Заметим, что для любых $a$ и $b$ справедливо:  $(a+b)^2\geq 4ab$.

Тогда

$log_{2016}2017\cdot log_{2016}2015\leq \frac{(log_{2016}2017+log_{2016}2015)^2}{4}=$

$=\frac{(log_{2016}(2017\cdot 2015))^2}{4}=\frac{(log_{2016}((2016+1)(2016-1)))^2}{4}=$

$=\frac{(log_{2016}(2016^2-1))^2}{4}\leq \frac{(log_{2016}2016^2)^2}{4}=1.$

Итак, $\frac{log_{2016}2017}{log_{2015}2016}\leq 1$, то есть $log_{2016}2017\leq log_{2015}2016$, а значит, $log_{2015}2016$ не входит в отрезок $[log_{2017}2016;log_{2016}2017].$

Ответ:

а) $1; log_{2015}2016.$

б) $1.$

a) Пусть радиус шара – $r.$ Тогда, согласно условию, высота конуса – $2r$.

Поскольку конус равносторонний (то есть осевое сечение конуса – правильный треугольник), то диаметр $d$ основания есть  $\frac{4r}{\sqrt3}$ (использовали тот факт, что сторона правильного треугольника с высотой $h$  есть $\frac{2h}{\sqrt3}$).

Имеем

$S_{shar}=4\pi r^2.$

$S_{konus}=S_{osnov}+S_{bok}=\pi\cdot (\frac{d}{2})^2+\pi\cdot (\frac{d}{2})\cdot d=\frac{3\pi d^2}{4}=4\pi r^2.$

Итак, $S_{shar}=S_{konus}.$

Что и требовалось доказать.

б) 

Рассмотрим осевое сечение конуса $ASB$.

Пусть $SH$ – высота конуса, пусть $CD$ – пересечение указанного осевого сечения и шара. Пусть $O$ – центр шара ($O$ – середина $SH$).

Так как $\angle ASH=30^{\circ}$, то $\angle COT=60^{\circ}.$  По свойству катета, лежащего напротив угла в $30^{\circ}$,  $OT=\frac{CO}{2}=\frac{r}{2}.$

Тогда $\frac{ST}{SH}=\frac{1,5r}{2r}=\frac{3}{4}.$

Назовем плоскость, по которой пересекаются поверхность шара и конус, за $\alpha.$

Объем $V_{1}$ той части конуса, что лежит внутри шара, складывается из объемов двух тел:

1) конуса, получаемого срезом исходного конуса плоскостью $\alpha$

2) малого шарового сегмента, отсекаемого от шара плоскостью $\alpha.$

Заметим при этом, что конус, получаемый срезом исходного конуса плоскостью $\alpha$, подобен исходному с коэффициентом подобия $\frac{3}{4}.$ Значит, объем его есть $\frac{27}{64}$ исходного.

Вспомним также формулу вычисления объема шарового сегмента (см. также здесь), которую несложно вывести:

$\color{red}V_{shar-segment}=\pi h^2(R-\frac{h}{3})$

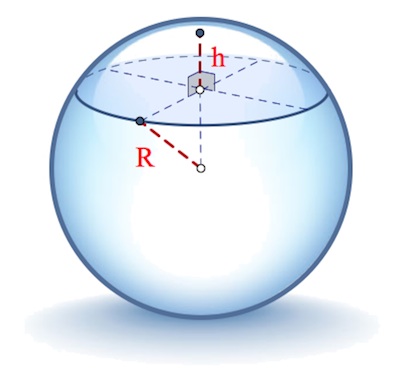
Итак,

$V_1=\frac{27}{64}\cdot \frac{\pi\cdot (\frac{2r}{\sqrt3})^2\cdot 2r}{3}+\pi (\frac{r}{2})^2(r-\frac{r}{6})=\frac{3\pi r^3}{8}+\frac{5\pi r^3}{24}=\frac{7\pi r^3}{12}.$

Объем же $V_2$ той части шара, что лежит вне конуса есть $V_{shar}-V_1$.

$V_2=\frac{4\pi r^3}{3}-\frac{7\pi r^3}{12}=\frac{9\pi r^3}{12}$.

Итак, $\frac{V_1}{V_2}=\frac{\frac{7\pi r^3}{12}}{\frac{9\pi r^3}{12}}=7:9$

Ответ: б) $7:9.$

$\sqrt{1+x^2}-x\leq \frac{5}{2\sqrt{1+x^2}};$

Заметим, $\sqrt{1+x^2}+x>0.$

Домножим обе части неравенства на $\sqrt{1+x^2}+x.$

$(\sqrt{1+x^2}-x)(\sqrt{1+x^2}+x)\leq \frac{5(\sqrt{1+x^2}+x)}{2\sqrt{1+x^2}};$

$1\leq \frac{5(\sqrt{1+x^2}+x)}{2\sqrt{1+x^2}};$

$2\sqrt{1+x^2}\leq 5(\sqrt{1+x^2}+x);$

$-5x\leq 3\sqrt{1+x^2};$

1) При  $x\geq 0$ последнее неравенство выполняется.

2) Рассмотрим случай $x<0$.

Возведем в квадрат обе части неравенства.

 $25x^2\leq 9(1+x^2);$

$16x^2\leq 9;$

$(4x-3)(4x+3)\leq 0;$

$x\in [-\frac{3}{4};\frac{3}{4}].$

С учетом того, что  $x<0$ имеем: $x\in [-\frac{3}{4};0).$

Итак, объединяя решения случаев (1) и (2), получаем следующее:

$x\in [-\frac{3}{4};+\infty).$

Ответ: $[-\frac{3}{4};+\infty).$

a) Пусть точки $P,T$ – точки касания окружности, вписанной в треугольник $ABE$, со сторонами $AB,AE$ соответственно.

Пусть точки $L,N$ – точки касания окружности, вписанной в треугольник $BCE$, со сторонами $BC,EC$ соответственно.

При решении будем использовать тот факт, что отрезки касательных, проведенных из одной точки к окружности, равны. Также, не забудем использовать, что $AB=BC.$

Рассмотрим случай, когда $AE\leq EC$.

$KM=BK-BM=BP-BL=(AB-AP)-(AB-LC)=LC-AP=$

$=NC-AT=(CE-EN)-(AE-TE)=(CE-EM)-$

$-(AE-EK)=(CE-AE)-(EM-EK)=(CE-AE)-KM.$

Итак, $KM=(CE-AE)-KM,$ то есть $KM=\frac{CE-AE}{2}.$

В случае, когда $AE>EC$, аналогичным образом получим: $KM=\frac{AE-CE}{2}.$

Итак, в общем случае имеем: $KM=\frac{1}{2}\cdot |CE-AE|$.

Что и требовалось доказать.

б) Пусть $r_1, r_2$ – радиусы окружностей $w_1,w_2$ соответственно.

Пусть $O$ – центр вписанной в  треугольник $ABC$ окружности, $H$ – точка касания указанной окружности с основанием $AC$. Пусть $O_1,O_2$ – центры вписанных окружностей $w_1,w_2$ соответственно.

Заметим, центр вписанной в треугольник окружности лежит на биссектрисах углов треугольника.

Очевидно, $AH=HC=\frac{9+15}{2}=12$ и $OH=4$ (как радиус вписанной окружности в $ABC$).

Пусть $\alpha =\frac{\angle C}{2}.$

Из треугольника $COH$:

$tg\alpha =\frac{4}{12}=\frac{1}{3}.$

Согласно пункту (a) задачи $KM=\frac{1}{2}\cdot |CE-AE|=3.$

Пусть $KE=TE=x$. Тогда $ME=EN=x+3.$ Стало быть, $AT=9-x, NC=12-x.$

Из треугольников $AO_1T,CO_2N:$

$tg\alpha=\frac{1}{3}=\frac{r_1}{9-x}=\frac{r_2}{12-x}.$

Откуда

$r_1=\frac{9-x}{3},r_2=\frac{12-x}{3}.$

Итак,

$r_2-r_1=\frac{(12-x)-(9-x)}{3}=1.$

Ответ: б) $1$.

Пусть имеется $x$ по объему меда и $x$ – дегтя.

Этап 1.

Пусть шутник  взял $y$ дегтя из второй банки (с дегтем) и добавил ее в банку с медом (первую), перемешал.

Во второй банке

$x-y$ дегтя, $o$ меда.

В первой банке

смеси – $x+y$

вес дегтя – $y$, вес меда – $x$

доля дегтя – $\frac{y}{x+y}$, доля меда – $\frac{x}{x+y}$

Этап 2.

Шутник  взял $y$ смеси из первой банки и добавил ее во вторую банку, перемешал.

В $y$ смеси от первой банки

вес дегтя – $\frac{y^2}{x+y}$, вес меда – $\frac{xy}{x+y}.$

В первой банке

смеси – $x$

вес дегтя – $y-\frac{y^2}{x+y}$ (или $\frac{xy}{x+y}$), вес меда – $x-\frac{xy}{x+y}$ (или $\frac{x^2}{x+y}$)

Во второй банке

смеси – $x$

вес дегтя – $x-y+\frac{y^2}{x+y}$ (или $\frac{x^2}{x+y}$), вес меда – $\frac{xy}{x+y}$

доля дегтя – $\frac{x}{x+y}$, доля меда – $\frac{y}{x+y}$

Этап 3.

Шутник  взял $y$ смеси из второй банки и добавил ее в первую банку, перемешал.

В $y$ смеси от второй банки

 вес дегтя – $\frac{xy}{x+y}$, вес меда – $\frac{y^2}{x+y}$

Во второй банке

смеси – $x-y$

вес дегтя – $\frac{x^2}{x+y}-\frac{xy}{x+y}$ (или $\frac{x(x-y)}{x+y}$), вес меда – $\frac{xy}{x+y}-\frac{y^2}{x+y}$ (или $\frac{y(x-y)}{x+y}$)

В первой банке

смеси – $x+y$

вес дегтя – $\frac{xy}{x+y}+\frac{xy}{x+y}$ (или $\frac{2xy}{x+y}$), вес меда – $\frac{x^2}{x+y}+\frac{y^2}{x+y}$ (или $\frac{x^2+y^2}{x+y}$)

доля дегтя – $\frac{2xy}{(x+y)^2}$, доля меда – $\frac{x^2+y^2}{(x+y)^2}$

Этап 4.

Шутник  взял $y$ смеси из первой банки и добавил ее во вторую банку, перемешал.

В $y$ смеси от первой банки

 вес дегтя – $\frac{2xy^2}{(x+y)^2}$, вес меда – $\frac{y(x^2+y^2)}{(x+y)^2}.$

В первой банке

смеси – $x$

вес дегтя – $\frac{2xy}{x+y}-\frac{2xy^2}{(x+y)^2}$ (или $\frac{2x^2y}{(x+y)^2}$)

доля дегтя – $\frac{2xy}{(x+y)^2}$

Во второй банке

смеси – $x$

вес меда – $\frac{y(x-y)}{x+y}+\frac{y(x^2+y^2)}{(x+y)^2}$ (или $\frac{2x^2y}{(x+y)^2}$)

доля меда – $\frac{2xy}{(x+y)^2}$

Итак, после манипуляций шутника доли меда в дегте и дегтя в меде оказались равными.

Ответ: дегтя в меде и меда в дегте оказалось поровну.

$\begin{cases}\sqrt{x^2+y^2+3(3-2|x|)}+\sqrt{y^2+y-a+8(2-|y|)}=5,\\y-x^2=a;&\end{cases}$

Из второй строки системы выражаем $y$ и подставляем в первую.

$\begin{cases}\sqrt{(|x|^2-6|x|+9)+y^2}+\sqrt{(|y|^2-8|y|+16)+x^2}=5,\\y-x^2=a;&\end{cases}$

$\begin{cases}\sqrt{(|x|-3)^2+y^2}+\sqrt{x^2+(|y|-4)^2}=5,\\y-x^2=a;&\end{cases}$

Рассмотрим сначала случай $x\geq 0,$  $y\geq 0$, то есть работаем в первой четверти координатной плоскости.

Уравнение $\sqrt{(x-3)^2+y^2}+\sqrt{x^2+(y-4)^2}=5$  задает отрезок с концами $(3;0),(0;4).$

Действительно, левая часть уравнения – есть сумма расстояний от некоторой точки $(x,y)$ до точек  $(3;0),(0;4).$ При этом расстояние между  точками $(3;0),(0;4)$ равно $\sqrt{(3-0)^2+(0-4)^2}=5$, а в правой части уравнения как раз и стоит $5$.

Работая во второй четверти, получим отрезок с концами $(-3;0),(0;4).$

И так далее.

То есть уравнение $\sqrt{(|x|-3)^2+y^2}+\sqrt{x^2+(|y|-4)^2}=5$ задает ромб (см. рис).

Уравнение же $y=x^2+a$ задает семейство парабол с вершиной $(0;a).$

За прохождение параболы $y=x^2+a$  через точку $(3;0)$ (или $(-3;0)$ отвечает $a=-9.$

За прохождение параболы $y=x^2+a$  через точку $(0;-4)$  отвечает $a=-4.$

За касание параболы с прямой $y=\frac{4x}{3}-4$ (или $y=\frac{-4x}{3}-4$) отвечает $a=-\frac{32}{9}.$

Действительно,

$D=0$  для  $\frac{4x}{3}-4=x^2+a$, если $a=-\frac{32}{9}.$

Итак, исходная система имеет ровно четыре решения, если

$a\in (-9;-4)\cup ${$-\frac{32}{9}$}.

(на рисунке красным цветом выделены зоны, располагаясь в которых, парабола будет иметь четыре пересечения с ромбом; пунктиром отмечены «открытые» границы)

Ответ: $(-9;-4)\cup ${$-\frac{32}{9}$}.